Transient Current

An electric current which vary for a small finite time, while growing from zero to maximum or decaying from maximum to zero, is called a transient current.

Growth of Current in an Inductor

Growth of current in an inductor at any instant of time t is given by

I = I_o(1 – e ^{-Rt / L})

where, I_o = maximum current, L = self inductance of the inductor and R = resistance of the circuit.

Here R / L = τ, is called time constant of a L – R circuit.

Time constant of a L – R circuit is the time in which current in the circuit grows to 63.2% of the maximum value of current.

Decay of current in an inductor at any time t is given by

I = I_oe ^{-Rt / L}

Time constant of a L – R circuit is the time in which current decays to 36.8% of the maximum value of current.

Charging and Discharging of a Capacitor

The instantaneous charge on a capacitor on charging at any instant of time t is given by

q = q_o(1 – e ^{– t / RC})

where RC = τ, is called time constant of a R – C circuit.

The instantaneous charge on a capacitor in discharging at any instant of time t is given by q = q_oe ^{– t / RC}

Time constant of a R – C circuit is the time in which charge in the capacitor grows to 63.8% or decay to 36.8% of the maximum charge on capacitor.

Alternating Current

An electric current whose magnitude changes continuously with time and changes its direction periodically, is called an alternating current.

The instantaneous value of alternating current at any instant of time t is given by

I = I_o sin ωt

where, 10 = peak value of alternating current.

The variation of alternating current with time is shown in graph given below

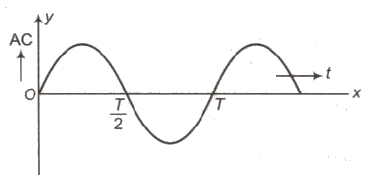
Mean or average value of alternating current for first half cycle

I_m = 2I_o / π = 0.637 I_o

Mean or average value of alternating current for next half cycle

I’_m = – 2I_o / π = – 0.637 I_o

Mean or average value of alternating current for one complete cycle = O.

Root mean square value of alternating current

I_v = I_rms = I_o / √2 = 0.707 I_o

Where, I_o = peak value of alternating current.

Root mean square value of alternating voltage

V_rms = V_o / √2 = 0.707 I_o = 0.707 V_o

Reactance

The opposition offered by an inductor or by a capacitor in the path of flow of alternating current is called reactance.

Reactance is of two types

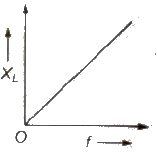
(i) Inductive Reactance (X_L) Inductive reactance is the resistance offered by an inductor.

Inductive reactance (X_L) = Lω = L2πf = L2π / T

Its unit is ohm. X_L ∝ f

For direct current, X_L = 0 (f = 0)

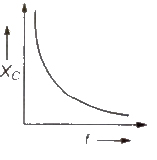
(ii) Capacitive Reactance (X_c) Capacitive reactance is the resistance offered by an inductor

Capacitive reactance,

X_c = 1 / Cω = 1 / C2πf = T / C 2π

Its unit is ohm X_c ∝ 1 / f

For direct current, X_c = ∞ (f = 0)

Impedance

The opposition offered by an AC circuit containing more than one out of three components L, C and R, is called impedance (Z) of the circuit.

Impedance of an AC circuit, Z = √R² + (X_L – X_C)²

Its SI unit is ohm.

Power in an AC Circuit

The power is defined as the rate at which work is being in the circuit.

The average power in an AC circuit,

P_av = V_rms i_rms cos θ

= V / √2 i / √2 cos θ = Vi / √2 cos θ

where, cos θ = Resistance(R) / Impedance (Z) is called the power factor 0f AC circuit.

Current and Potential Relations

Here, we will discuss current and potential relations for different AC circuits.

(i) Pure Resistive Circuit (R circuit)

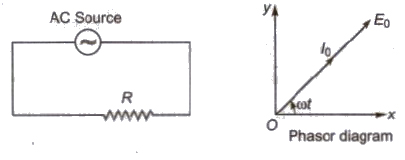
(a) Alternating emf, E = E_o sin ωt

(b) Alternating current, I = I_o sin ωt

(c) Alternating emf and alternating current both are in the same phase.

(d) Average power decay, (P) = E_v . I_v

(e) Power factor, cos θ = 1

(ii) Pure Inductive Circuit (L Circuit)

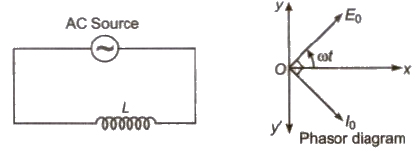
(a) Alternating emf, E = E_o sin ωt

(b) Alternating current, I = I_o sin (ωt – π / 2)

(c) Alternating current lags behind alternating emf by π / 2.

(d) Inductive reactance, X_L = Lω = L2πf

(e) Average power decay, (P) = 0

(f) Power factor, cos θ = cos 90° = 0

(iii) Pure Capacitive Circuit

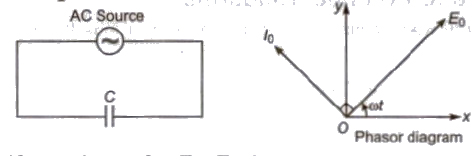
(a) Alternating emf, E = E_o sin ωt

(b) Alternating current, I = I_o sin (ωt + π / 2)

(c) Alternating current lags behind alternating emf by π / 2.

(d) Inductive reactance, X_L = Cω = C2πf

(e) Average power decay, (P) = 0

(f) Power factor, cos θ = cos 90° = 0

(iv) R – C Circuit

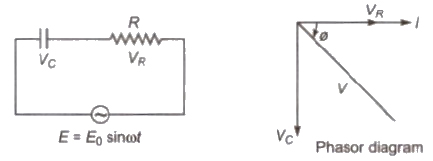
E = E_o sin ωt

I = E_o / 2 sin (ωt – φ)

Z = √R² + (1 / ωC)²

tan φ = – 1 / ωC / R

Current leading the voltage by φ

V² = V²_R = V²_C

(v) L – C Circuit

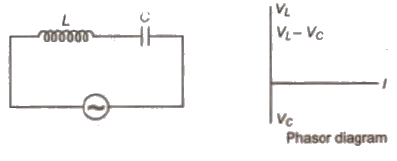
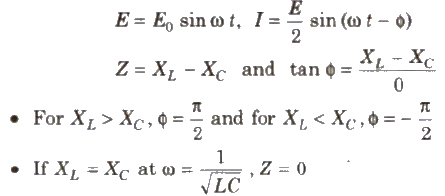
(vi) L – C – R Circuit

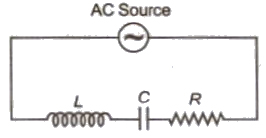
(a) Alternating emf, E = E_o sin Ωt

(b) Alternating current, I = I_o sin (Ωt ± θ)

(c) Alternating current lags leads behind alternating emf by ω.

(d) Resultant voltage, V = √V²_R + (V_L – V_C)²

(e) Impedance, Z = √R² + (X_L – X_C)²

(f) Power factor, cos θ = R / Z = R / √√R² + (X_L – X_C)²

(g) Average power decay, (P)= E_VI_V cos θ

Resonance in AC Circuit

The condition in which current is maximum or impedance is minimum in an AC circuit, is called resonance.

(i) Series Resonance Circuit

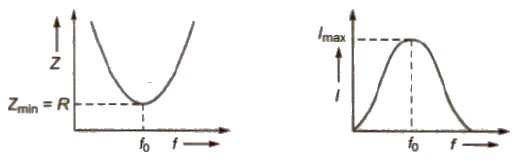
In this circuit components L, C and R are connected in series.

At resonance = X_L = X_C

Resonance frequency f = 1 / 2π√LC

A series resonance circuit is also known as acception circuit.

(ii) Parallel Resonance Circuit

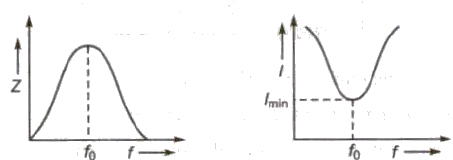
In this circuit L and C are connected in parallel with each other.

At resonance, X_L = X_C

Impedance (Z) of the circuit is maximum.

Current in the circuit is minimum.

Wattless Current

Average power is given by

P_av = E_rms = I_rms cos θ

Here the I_rms cos φ contributes for power dissipation. Therefore, it is called wattless current.

AC Generator or Dynamo

It is a device which converts mechanical energy into alternating current energy.

Its working is based on electromagnetic induction.

The induced emf produced by the AC generator is given by

e = NBAω sin ωt = e_o = sin ωt

There are four main parts of an AC generator

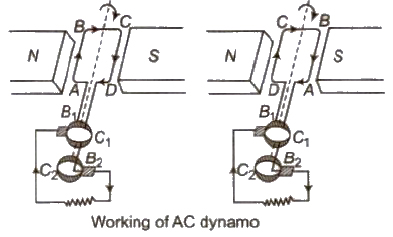
(i) Armature It is rectangular coil of insulated copper wire having a large number of turns.

(ii) Field Magnets These are two pole pieces of a strong electromagnet.

(iii) Slip Rings These are two hollow metallic rings.

(iv) Brushes These are two flexible metals or carbon rods, which remains slightly in contact with slip rings .

Note An DC generator or dynamo contains split rings or commutator inspite of slip rings.

DC Motor

It is a device which converts electrical energy into mechanical energy.

Its working is based on the fact that when a current carrying coil is placed in uniform magnetic field a torque acts on it.

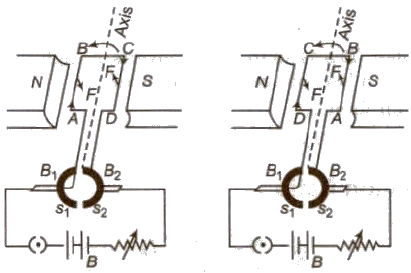
Torque acting on a current carrying coil placed in uniform magnetic field

τ = NBIA sin θ

When armature coil rotates a back emf is produced in the coil.

Efficiency of a motor,

η = Back emf / Applied emf = E / V

Transformer

It is a device which can change a low voltage of high current into a high voltage of low current and vice-versa.

Its working is based on mutual induction.

There are two types of transformers.

(i) Step-up Transformers It converts a low voltage of high current into a high voltage of low current.

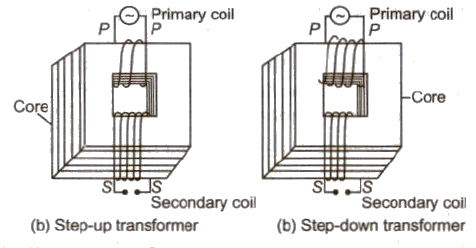
In this transformer,

N_s > N_P, E_s > E_P

and I_P > I_S

(ii) Step-down Transformer It converts a high voltage of low current into a low voltage of high current.

In this transformer,

N_P > N_S, E_P > E_S and I_P < I_S

Transformation Ratio

Transformation ratio,

K = N_S / N_P = E_S / E_P = I_P / I_S

For step-up transformer, K > 1

For step-down transformer, K < 1

Energy Losses in a Transformer

The main energy losses in a transformer are given below

1. Iron loss
2. Copper loss
3. Flux loss
4. Hysteresis loss
5. Humming loss

Important Points

• Transformer does not operate on direct current. It operates only on alternating voltages at input as well as at output.
• Transformer does not amplify power as vacuum tube.
• Transformer, a device based on mutual induction converts magnetic energy into electrical energy.
• Efficiency, η = Output power / Input power

Generally efficiency ranges from 70% to 90%.

• A choke coil is a pure inductor. Average power consumed per cycle is zero in a choke coil.
• A DC motor connects DC energy from a battery into mechanical energy of rotation.
• An AC dynamo/generator produces are energy from mechanical energy of rotation of a coil.
• An induction coil generates high voltages of the order of 1OS V from a battery.

It is based on the phenomenon of mutual induction.