Surface tension is the property of any liquid by virtue of which tries to minimize its free surface area.

Surface tension of a liquid is measured as the force acting per length on an imaginary line drawn tangentially on the free surface the liquid.

Surface tension S = Force/Length = F/l = Work done/Change in area

Its SI unit is Nm^-1 or Jm^-2 and its dimensional formula is [MT^-2].

It is a scalar quantity. Surface tension is a molecular phenomenon which is due to cohesive force and root cause of the force is electrical in nature.

Surface tension of a liquid depends only on the nature of liquid and independent of the surface area of film or length of the line .

Small liquid drops are spherical due to the property of surface tension.

Adhesive Force

The force of attraction acting between the molecules of different substances is called adhesive force, e.g., the force of attracts acting between the molecules of paper and ink, water and glass, etc.

Cohesive Force

The force of attraction acting between the molecules of same substan is called cohesive force. e.g., the force of attraction acting between molecules of water, glass, etc.

Cohesive forces and adhesive forces are van der Waals’ forces.

These forces varies inversely as the seventh power of distance between the molecules.

Molecular Range

The maximum distance upto which a molecule can exert a force of attraction on other molecules is called molecular range.

Molecular range is different for different substances. In solids and liquids it is of the order of 10^-9 m.

If the distance between the molecules is greater than 10-9 m, the force of attraction between them is negligible.

Surface Energy

If we increase the free surface area of a liquid then work has to be done against the force of surface tension. This work done is stored in liquid stu-face as potential energy,

This additional potential energy per unit area of free surface of liquid is called surface energy.
Surface energy (E) = S x &ΔM
where. S = surface tension and ΔA = increase in surface area.

(i) Work Done in Blowing a Liquid Drop If a liquid drop is blown up from a radius r₁ to r₂ then work done for that is
W = S . 4π (r₂² – r₁²)

(ii) Work Done in Blowing a Soap Bubble As a soap bubble has two free surfaces, hence work done in blowing a soap bubble so as to increase its radius from r¹ to r² is given by
W = S.8π(r₂² – r₁²)

(iii) Work Done in Splitting a Bigger Drop into n Smaller Droplets
If a liquid drop of radius R is split up into n smaller droplets, all of same size. then radius of each droplet

r = R. (n)^-1/3
Work done, W = 4π(nr² – R²)
= 4πSR² (n^1/3 – 1)

(iv) Coalescance of Drops If n small liquid drops of radius reach combine together so as to form a single bigger drop of radius R=n^1/3.r, then in the process energy is released. Release of energy is given by

ΔU = S.4π(nr² – R²)

= 4πSπn(1 – n^1/3)

Angle of Contact

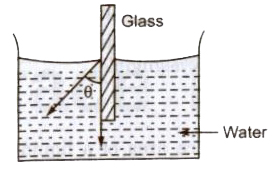
The angle subtended between the tangents drawn at liquid surface at solid surface inside the liquid at the point of contact, is called of contact (9).

Angle of contact depends upon the nature of the liquid and solid contact and the medium which exists above the free surface of liquid.

When wax is coated on a glass capillary tube, it becomes water-proof.
The angle of contact increases and becomes obtuse. Water does not in it. Rather it falls in the tube by virtue of obtuse angle of contact.

If θ is acute angle, i.e; θ <90°, then liquid meniscus will be concave upwards.

• If θ is 90°, then liquid meniscus will be plane.
• If θ is obtuse, i.e; θ >90°, then liquid meniscus will be convex upwards.
• If angle of contact is acute angle, i.e; θ <90°, then liquid will wet the surface.
• If angle of contact is obtuse angle, ie; θ > 90°, then liquid will not wet the surface.

Angle of contact increases with increase in temperature of Angle of contact decreases on adding soluble impurity to a liquid.

Angle of contact for pure water and glass is zero. For ordinary water and glass is 8°. For mercury and glass is 140°. For pure water silver is 90°. For alcohol and clean glass θ = 0°.

Angle of contact, meniscus, shape of liquid surface

Capillarity

The phenomenon called capillarity. of rise or fall of liquid column in a capillary tube is Ascent of a liquid column in a capillary tube is given by

h = (2S cos θ / rρg) – (r / 3)

If capillary is very narrow, then

h=2S cos θ / rρg

where, r = radius of capillary tube, p = density of the liquid, and
θ = angle of contact and S = surface tension of liquid.

• If θ < 90°, cos e is positive, so h is positive, i.e., liquid rises in a capillary tube.
• If θ > 90°, cos 9 is negative, so h is negative, i.e., liquid falls in a capillary tube.
• Rise of liquid in a capillary tube does not violate law of conservation of energy.

Some Practical Examples of Capillarity

1. The kerosene oil in a lantern and the melted wax in a candle, rise in the capillaries formed in the cotton wick and burns.
2. Coffee powder is easily soluble in water because water immediately wets the fine granules of coffee by the action of capillarity.
3. The water given to the fields rises in the innumerable capillaries formed in the stems of plants and trees and reaches the leaves.

Zurin’s Law

If a capillary tube of insufficient length is placed vertically in a then liquid never come out from the tube its own, as

Rh = constant ⇒ R₁h₁ = R₂h₂

where, R = radius of curvature of liquid meniscus and
h = height of liquid column.

When a tube is kept in inclined position in a liquid the vertical height remains unchanged then length of liquid column.

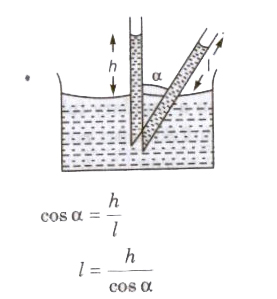
Liquid rises (water in glass capillary) or falls (mercury in capillary) due to property of surface tension

T = Rρgh / 2 cos θ

where, R = radius of capillary tube, h = height of liquid, p = density of liquid, e = angle of contact,

T = surface tension of liquid and 9 = acceleration due to gravity.

Excess Pressure due to Surface Tension

(i) Excess pressure inside a liquid drop = 2S / R

(ii) Excess pressure inside an air bubble in a liquid = 2S / R

(iii) Excess pressure inside a soap bubble = 4S / R

where, S = surface tension and R = radius of drop/bubble.

(iv) Work done in spraying a liquid drop of radius R into n droplets of radius r = T x increase in surface area

= 4πTR³ (1/r – 1/R)

Fall in temperature

Δθ = 3T/J (1/r – 1/R)

where. J = 4.2 J/cal.

(v) When n small drops are combined into a bigger drop, then work done is given by

W = 4πR²T (n ^1/3 – 1)

Temperature increase

Δθ = 3T/J (1/r – 1/R)

(vi) When two bubbles of radii r₁ and r₂ coalesce into a bubble of radius r isothermally, then
r² = r₁2 + r₂²

(vii) When two soap bubbles of radii ‘1 and ‘2 are in contact with each other, then radius (r) of common interface.

Factors Affecting Surface Tension

1. Surface tension of a liquid decreases with increase temperature and becomes zero at critical temperature.
2. At boiling point, surface tension of a liquid becomes zero becomes maximum at freezing point.
3. Surface tension decreases when partially soluble impurities such as soap, detergent, dettol, phenol, etc are added in water.
4. Surface tension increases when highly soluble impurities such as salt is added in water.
5. When dust particles or oil spreads over the surface of water, its surface tension decreases.

When charge is given to a soap bubble, its size increases surface tension of the liquid decreases due to electrification.

In weightlessness condition liquid does not rise in a capillary tube.

Some Phenomena Based on Surface Tension

1. Medicines used for washing wounds, as detol, have a surface tension lower than water.
2. Hot soup is more tasteful than the cold one because the surface tension of the hot soup is less than that of the cold and so spreads over a larger area of the tongue.
3. Insects and mosquitoes swim on the surface of water in ponds and lakes due to surface tension. If kerosence oil is sprayed on the water surface, the surface tension of water is lowered and the insects and mosquitoes sink in water and are dead.
4. If we deform a liquid drop by pushing it slightly, then due to surface tension it again becomes spherical.