Viscosity

The property of a fluid by virtue of which an internal frictional force acts between its different layers which opposes their relative motion is called viscosity.

These internal frictional force is called viscous force.

Viscous forces are intermolecular forces acting between the molecules of different layers of liquid moving with different velocities.

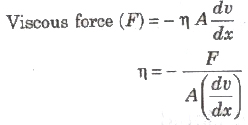
where, (dv/dx) = rate of change of velocity with distance called velocity gradient, A = area of cross-section and = coefficient of viscosity.

SI unit of η is Nsm^-2 or pascal-second or decapoise. Its dimensional formula is [ML^-1T^-1].

The knowledge of the coefficient of viscosity of different oils and its variation with temperature helps us to select a suitable lubricant for a given machine.

Viscosity is due to transport of momentum. The value of viscosity (and compressibility) for ideal liquid is zero.

The viscosity of air and of some liquids is utilised for damping the n.ving parts of some instruments.

The knowledge of viscosity of some organic liquids is used in determining the molecular weight and shape of large organic moleculars like proteins and cellulose.

Variation of Viscosity

The viscosity of liquids decreases with increase in temperature

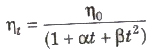
where, η₀ and η_t is are coefficient of viscosities at 0°C t°C, α and β are constants.

The viscosity of gases increases with increase in temperatures as

η ∝ √T

The viscosity of liquids increases with increase in pressure but the viscosity of water decreases with increase in pressure.

The viscosity of gases do not changes with pressure.

Poiseuille’s Formula

The rate of flow (v) of liquid through a horizontal pipe for steady flow is given by

where, p = pressure difference across the two ends of the tube. r = radius of the tube, n = coefficient of viscosity and 1 = length of th tube.

The Rate of Flow of Liquid

Rate of flow of liquid through a tube is given by

v = (P/R)

where, R = (8 ηl/πr⁴), called liquid resistance and p = liquid pressure.

(i) When two tubes are connected in series

• Resultant pressure difference p = p₁ + p₂
• Rate of flow of liquid (v) is same through both tubes.
• Equivalent liquid resistance, R = R₁ + R₂

(ii) When two tubes are connected in parallel

1. Pressure difference (p) is same across both tubes.
2. Rate of flow of liquid v = v₁ + v₂
3. Equivalent liquid resistance (1/R) = (1/R₁) + (1/R₂)

Stoke’s Law

When a small spherical body falls in a long liquid column, then after sometime it falls with a constant velocity, called terminal velocity. When a small spherical body falls in a liquid column with terminal velocity then viscous force acting on it is

F = 6πηrv

where, r = radius of the body, V = terminal velocity and η = coefficient of viscosity.

This is called Stoke’s law.

where,

• ρ = density of body,
• σ = density of liquid,
• η = coefficient of viscosity of liquid and,
• g = acceleration due to gravity

1. If ρ > ρ₀, the body falls downwards.
2. If ρ < ρ₀, the body moves upwards with the constant velocity.
3. If po << ρ, v = (2r²ρg/9η)

Importance of Stoke’s Law

1. This law is used in the determination of electronic charge by Millikan in his oil drop experiment.
2. This law helps a man coming down with the help of parachute.
3. This law account for the formation of clouds.

Flow of Liquid

1. Streamline Flow The flow of liquid in which each of its particle follows the same path as followed by the proceeding particles, is called streamline flow.
2. Laminar Flow The steady flow of liquid over a horizontal surface in the form of layers of different velocities, is called laminar flow.
3. Turbulent Flow The flow of liquid with a velocity greater than its critical velocity is disordered and called turbulent flow.

Critical Velocity

The critical velocity is that velocity of liquid flow, below which its fl is streamlined and above which it becomes turbulent.

Critical velocity v_c = (k_η/rρ)

where,

• K = Reynold’s number,
• η = coefficient of viscosity of liquid
• r = radius of capillary tube and ρ = density of the liquid.

Reynold’s Number

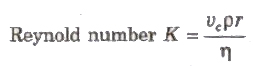
Reynold’s number is a pure number and it is equal to the ratio of inertial force per unit area to the viscous force per unit area for flowing fluid.

where, p = density of the liquid and v_c = critical velocity.

For pure water flowing in a cylindrical pipe, K is about 1000.

When 0< K< 2000, the flow of liquid is streamlined.

When 2000 < K < 3000, the flow of liquid is variable betw streamlined and turbulent.

When K > 3000, the flow of liquid is turbulent.

It has no unit and dimension.

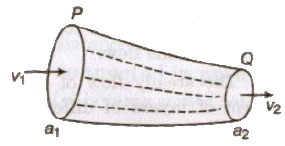
Equation of Continuity

If a liquid is flowing in streamline flow in a pipe of non-unif cross-section area, then rate of flow of liquid across any cross-sec remains constant.

a₁v₁ = a₂v₂ av = constant

The velocity of liquid is slower where area of cross-section is larger faster where area of cross-section is smaller.

The falling stream of water becomes narrower, as the velocity of f stream of water increases and therefore its area of cross-s decreases.

Energy of a Liquid

A liquid in motion possess three types of energy

(i) Pressure Energy Pressure energy per unit mass = p/ρ

where,

p= pressure of the liquid and p = density of the liquid.
Pressure energy per unit volume = p

(ii) Kinetic Energy

• Kinetic energy per unit mass = (1/2v²)
• Kinetic energy per unit volume = 1/2ρv²

(iii) Potential Energy

• Potential energy per unit mass = gh
• Potential energy per unit volume = ρgh

Bernoulli’s Theorem

If an ideal liquid is flowing in streamlined flow then total energy, i.e., sum of pressure energy, kinetic energy and potential energy per unit
volume of the liquid remains constant at every cross-section of the tube.

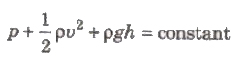
Mathematically

It can be expressed as

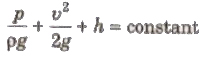
where, (p/ρg) = pressure head, (v²/2g) = velocity head and h = gravitational head.

For horizontal flow of liquid,

• where, pis called static pressure and (1/2 ρv²) is called dynamic pressure.
• The erefore in horizontal flow of liquid, if p increases, v decreases and Nce-versa.
• The theorem is applicable to ideal liquid, i.e., a liquid which is non-viscous incompressible and irrotational.

Applications of Bernoulli’s Theorem

1. The action of carburetor, paintgun, scent sprayer atomiser insect sprayer is based on Bernoulli’s theorem.
2. The action of Bunsen’s burner, gas burner, oil stove exhaust pump is also based on Bernoulli’s theorem.
3. Motion of a spinning ball (Magnus effect) is based on Bernoulli theorem.
4. Blowing of roofs by wind storms, attraction between two close parallel moving boats, fluttering of a flag etc are also based Bernoulli’s theorem.

Venturimeter

It is a device used for measuring the rate of flow of liquid t pipes. Its working is based on Bernoulli’s theorem.

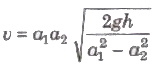
Rate of flow of liquid,

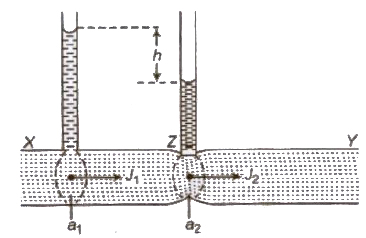
where, a₁ and a₂ are area of cross-sections of tube at bra and narrower part and h is difference of liquid columns in ver tubes.

Torricelli’s Theorem

Velocity of efflux (the velocity with which the liquid flows out orifice or narrow hole) is equal to the velocity acquired by a falling body through the same vertical distance equal to the dep orifice below the free surface of liquid.

Velocity of efflux, v = √2gh

where, h = depth of orifice below the free surface of liquid.

Horizontal range, S = √4h(H — h)

where, H = height of liquid column.

Horizontal range is maximum, equal to height of the liquid column H, when orifice is at half of the height of liquid column.

Important Points

• In a pipe the inner layer .central layer) have maximum velocity and the layer in contact with pipe have least velocity.
• Velocity profile of liquid flow in a pipe is parabolic.
• Solid friction is independent of area of surfaces in contact while viscous force depends on area of liquid layers.
• A lubricant is chosen ac:ording to the nature of machinary. In heavy machines lubricating oils of high viscosity are used and in light machines low viscosity oils are used.
• The cause of viscosity 1 liquids is the cohesive forces among their molecules while cause of viscosity in gases is diffusion.