





Centre of Mass
Centre of mass of a system is the point that behaves as whole mass of the system is concentrated at it and all external forces are acting on it.
For rigid bodies, centre of mass is independent of the state of the body i.e., whether it is in rest or in accelerated motion centre of mass will rermain same.
Centre of Mass of System of n Particles
If a system consists of n particles of masses m1, m2, m3 ,… mn having position vectors rl, r2, r3,… rn. then position vector of centre of mass of

Centre of Mass of Two Particle System
Choosing O as origin of the coordinate axis.
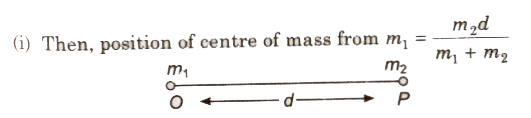
(ii) Position of centre of mass from m2 = (m1d) / m1 + m2
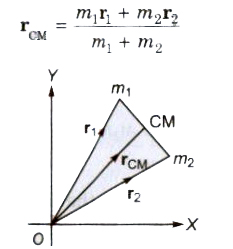
iii) If position vectors of particles of masses m1 and m2 are r1 and r2respectively, then
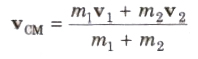
(iv) If in a two particle system, particles of masses m1 and m2 moving with velocities v1 and v2 respectively, then velocity the centre of mass
(v) If accelerations of the particles are a1, and a1respectively, then acceleration of the centre of mass
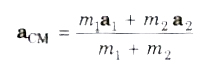
(vi) Centre of mass of an isolated system has a constant velocity.
(vii) It means isolated system will remain at rest if it is initially rest or will move with a same velocity if it is in motion initially.
(viii) The position of centre of mass depends upon the shape, size and distribution of the mass of the body.
(ix) The centre of mass of an object need not to lie with in the object.
(x) In symmetrical bodies having homogeneous distribution mass the centre of mass coincides with the geometrical centre the body.
(xi) The position of centre of mass of an object changes translatory motion but remains unchanged in rotatory motion,
Translational Motion
A rigid body performs a pure translational motion, if each particle the body undergoes the same displacement in the same direction in given interval of time.
Rotational Motion
A rigid body performs a pure rotational motion, if each particle of the body moves in a circle, and the centre of all the circles lie on a straight line called the axes of rotation.
Rigid Body
If the relative distance between the particles of a system do not changes on applying force, then it called a rigtd body. General motion of a rigid body consists of both the translational motion and the rotational motion.
Moment of Inertia
The inertia of rotational motion is called moment of inertia. It is denoted by L.
Moment of inertia is the property of an object by virtue of which it opposes any change in its state of rotation about an axis.
The moment of inertia of a body about a given axis is equal to the sum of the products of the masses of its constituent particles and the square of their respective distances from the axis of rotation.
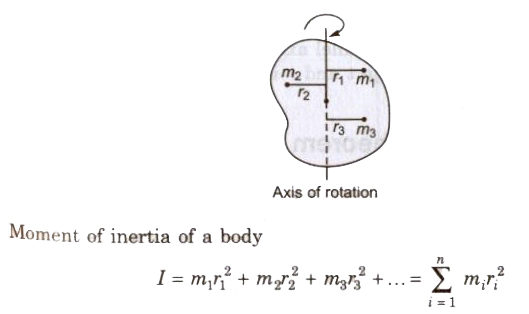
Its unit is kg.m2 and its dimensional formula is [ML2].
The moment of inertia of a body depends upon
The physical significance of the moment of inertia is same in rotational motion as the mass in linear motion.
The Radius of Gyration
The root mean square distance of its constituent particles from the axis of rotation is called the radius of gyration of a body.
It is denoted by K.
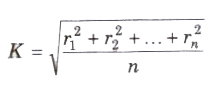
Radius of gyration
The product of the mass of the body (M) and square of its radius gyration (K) gives the same moment of inertia of the body about rotational axis.
Therefore, moment of inertia I = MK2 ⇒ K = √1/M
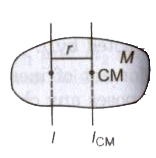
Parallel Axes Theorem
The moment of inertia of any object about any arbitrary axes is equal to the sum of moment of inertia about a parallel axis passing through the centre of mass and the product of mass of the body and the square of the perpendicular distance between
the two axes.
Mathematically I = ICM + Mr2
where I is the moment of inertia about the arbitrary axis, IcM is moment of inertia about the parallel axis through the centre of mass, M is the total mass of the object and r is the perpendicular distance between the axis.

Perpendicular Axes Theorem
The moment of inertia of any two dimensional body about an axis perpendicular to its plane (Iz) is equal to the sum of moments of inertia of the body about two mutually perpendicular axes lying in its own plane and intersecting
each other at a point, where the perpendicular axis passes through it.
Mathematically Iz = Ix + Iy
where Ix and Iy are the moments of inertia of plane lamina about perpendicular axes X and Y respectively which lie in the plane lamina an intersect each other.
Theorem of parallel axes is applicable for any type of rigid body whether it is a two dimensional or three dimensional, while the theorem of perpendicular is applicable for laminar type or two I dimensional bodies only.
Moment of Inertia of Homogeneous Rigid Bodies
For a Thin Circular Ring
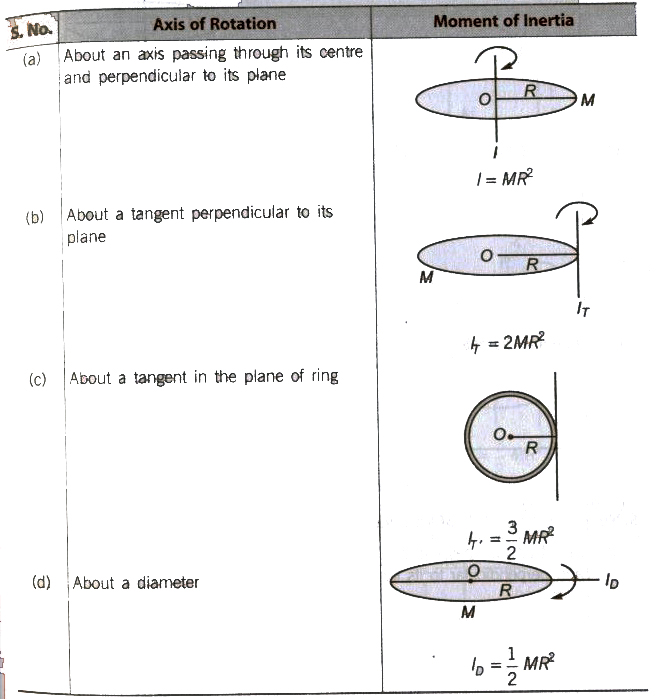
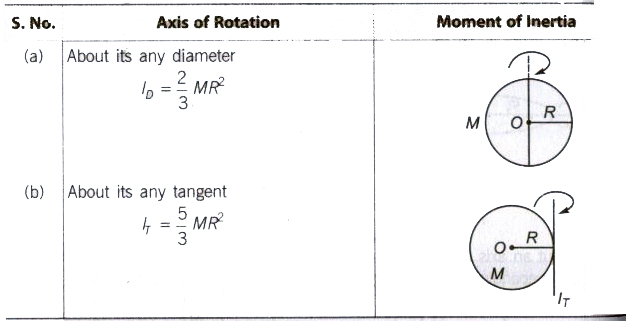
For a Circular Disc

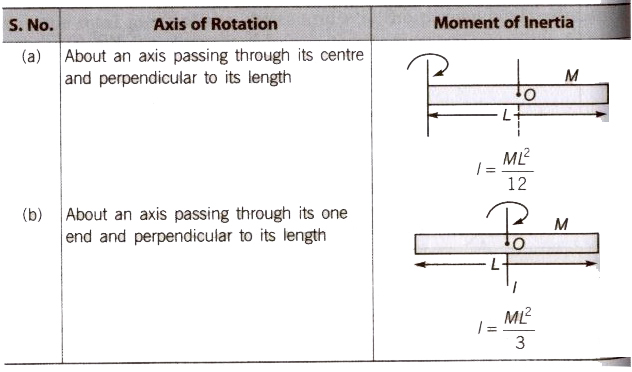
For a Thin Rod
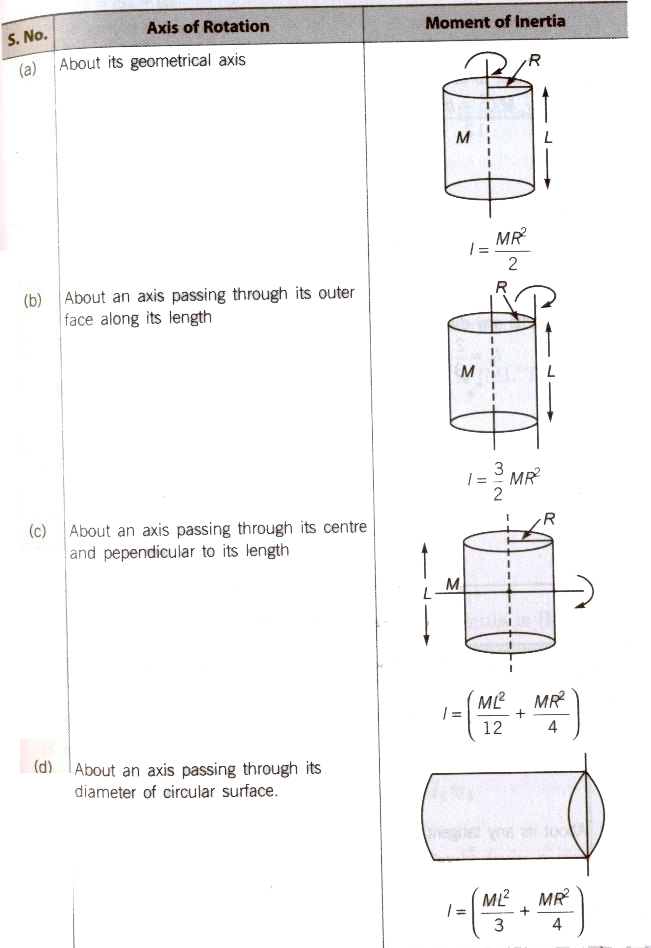
For a Solid Cylinder
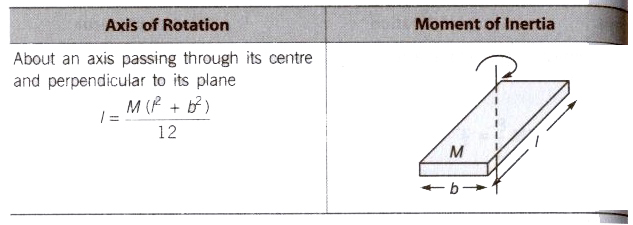
For a Rectangular Plate
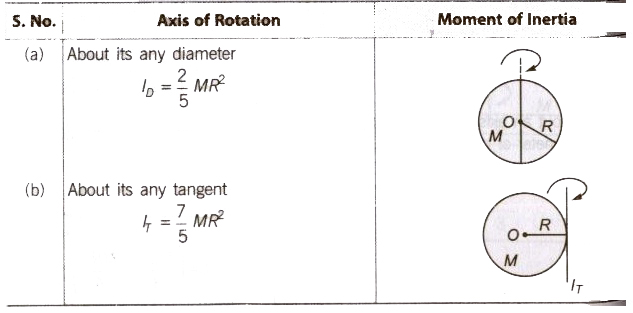
For a Thin Spherical Shell
For a Solid Sphere
Equations of Rotational Motion
(i) ω = ω0 + αt
(ii) θ = ω0t + 1/2 αt2
(iii) ω2 = ω02 + 2αθ
where θ is displacement in rotational motion, ω0 is initial velocity, omega; is final velocity and a is acceleration.
Torque
Torque or moment of a force about the axis of rotation
τ = r x F = rF sinθ n
It is a vector quantity.
If the nature of the force is to rotate the object clockwise, then torque is called negative and if rotate the object anticlockwise, then it is called positive.
Its SI unit is ‘newton-metre’ and its dimension is [ML2T-2].
In rotational motion, torque, τ = Iα
where a is angular acceleration and 1is moment of inertia.
Angular Momentum
The moment of linear momentum is called angular momentum.
It is denoted by L.
Angular momentum, L = I ω = mvr
In vector form, L = I ω = r x mv
Its unit is ‘joule-second’ and its dimensional formula is [ML2T-1].
Torque, τ = dL/dt
Conservation of Angular Momentum
If the external torque acting on a system is zero, then its angular momentum remains conserved.
If τext 0, then L = I(ω) = constant ⇒ I1ω1== I2ω2
Angular Impulse
Total effect of a torque applied on a rotating body in a given time is called angular impulse. Angular impulse is equal to total change in angular momentum of the system in given time. Thus, angular impulse
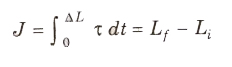
.png)