





Work
When a force acts on an object and the object actually moves in the direction of force, then the work is said to be done by the force.
Work done by the force is equal to the product of the force and the displacement of the object in the direction of force.
If under a constant force F the object displaced through a distance s, then work done by the force
W = F * s = F s cos θ
where a is the smaller angle between F and s.
Work is a scalar quantity, Its S1 unit is joule and CGS unit is erg.
∴ 1 joule = 107 erg
Its dimensional formula is [ML2T-2].
Work done by a force is zero, if
(a) body is not displaced actually, i.e., s = 0
(b) body is displaced perpendicular to the direction of force, i.e.,
θ = 90°
Work done by a force is positive if angle between F and s is acute angle.
Work done by a force is negative if angle between F and s is obtuse angle.
Work done by a constant force depends only on the initial and final Positions and not on the actual path followed between initial and final positions.
Work done in different conditions
(i) Work done by a variable force is given by
W = ∫ F * ds
It is equal to the area under the force-displacement graph along with proper sign.
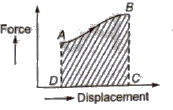
Work done = Area ABCDA
(ii) Work done in displacing any body under the action of a number of forces is equal to the work done by the resultant force.
(iii) In equilibrium (static or dynamic), the resultant force is zero therefore resultant work done is zero.
(iv) If work done by a force during a rough trip of a system is zero, then the force is conservative, otherwise it is called non-conservative force.
(v) Work done by the force of gravity on a particle of mass m is given by W = mgh
where g is acceleration due to gravity and h is height through particle one displaced.
(vi) Work done in compressing or stretching a spring is given by
W = 1 / 2 kx2
where k is spring constant and x is displacement from mean position.
(vii) When on end of a spring is attached to a fixed vertical support and a block attached to the free end moves on a horizontal
table from x = x1 to x = x2 then W = 1 / 2 k (x2x2 – x2x1)
(viii) Work done by the couple for an angular displacement θ is given by W = i * θ
where i is the torque of the couple.
power
The time rate of work done by a body is called its power.
Power = Rate of doing work = Work done / Time taken
If under a constant force F a body is displaced through a distance s in time t, the power
p = W / t = F * s / t
But s / t = v ; uniform velocity with which body is displaced.
∴ P = F * v = F v cos θ
where θ is the smaller angle between F and v.
power is a scalar quantity. Its S1 unit is watt and its dimensional formula is [ML2T-3].
Its other units are kilowatt and horse power,
1 kilowatt = 1000 watt
1 horse power = 746 watt
Energy
Energy of a body is its capacity of doing work.
It is a scalar quantity.
Its S1 unit is joule and CGS unit is erg. Its dimensional formula is [ML3T-3].
There are several types of energies, such as mechanical energy (kinetic energy and potential energy), chemical energy, light energy, heat energy, sound energy, nuclear energy, electric energy etc.
Mechanical Energy
The sum of kinetic and potential energies at any point remains constant throughout the motion. It does not depend upon time. This is known as law of conservation of mechanical energy.
Mechanical energy is of two types:
1. Kinetic Energy
The energy possessed by any object by virtue of its motion is called its kinetic energy.
Kinetic energy of an object is given by
k = 1 / 2 mv2 = p2 / 2m
where m = mass of the object, U = velocity of the object and p = mv = momentum of the object.
2. Potential Energy
The energy possessed by any object by virtue of its position or configuration is called its potential energy.
There are three important types of potential energies:
(i) Gravitational Potential Energy If a body of mass m is raised through a height h against gravity, then its gravitational potential energy = mgh,
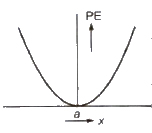
(ii) Elastic Potential Energy If a spring of spring constant k is stretched through a distance x. then elastic potential energy of the spring = 1 . 2 kx2
The variation of potential energy with distance is shown in figure.
Potential energy is defined only for conservative forces. It does not exist for non-conservative forces.
Potential energy depends upon frame of reference.
(iii) Electric Potential Energy The electric potential energy of two point charges ql and q’l. separated by a distance r in vacuum is given by
U = 1 / 4πΣ0 * q1q2 / r
Here 1 / 4πΣ0 = 9.0 * 1010 N-m2 / C2 constant.
Work-Energy Theorem
Work done by a force in displacing a body is equal to change in its kinetic energy.

where, Ki = initial kinetic energy
and Kf = final kinetic energy.
Regarding the work-energy theorem it is worth noting that
(i) If Wnet is positive, then Kf – Ki = positive, i.e., Kf > Ki or kinetic energy will increase and vice-versa.
(ii) This theorem can be applied to non-inertial frames also. In a non-inertial frame it can be written as:
Work done by all the forces (including the Pseudo force) = change in kinetic energy in non-inertial frame.
Mass-Energy Equivalence
According to Einstein, the mass can be transformed into energy and vice – versa.
When Δm. mass disappears, then produced energy
E = Δmc2
where c is the speed of light in vacuum.
Principle of Conservation of Energy
The sum of all kinds of energies in an isolated system remains constant at all times.
Principle of Conservation of Mechanical Energy
For conservative forces the sum of kinetic and potential energies of any object remains constant throughout the motion.
According to the quantum physics, mass and energy are not conserved separately but are conserved as a single entity called ‘mass-energy’.
Collisions
Collision between two or more particles is the interaction for a short interval of time in which they apply relatively strong forces on each other.
In a collision physical contact of two bodies is not necessary. rrhere are two types of collisions:
1. Elastic collision
The collision in which both the momentum and the kinetic energy of the system remains conserved are called elastic collisions.
In an elastic collision all the involved forces are conservative forces.
Total energy remains conserved.
2. Inelastic collision
The collision in which only the momentum remains conserved but kinetic energy does not remain conserved are called inelastic collisions.
In an inelastic collision some or all the involved forces are non-conservative forces.
Total energy of the system remains conserved.
If after the collision two bodies stick to each other, then the collision is said to be perfectly inelastic.
Coefficient of Restitution or Resilience
The ratio of relative velocity of separation after collision to the velocity of approach before collision is called coefficient of restitution resilience.
It is represented by e and it depends upon the material of the collidingI bodies.
For a perfectly elastic collision, e = 1
For a perfectly inelastic collision, e = 0
For all other collisions, 0 < e < 1
One Dimensional or Head-on Collision
If the initial and final velocities of colliding bodies lie along the same line, then the collision is called one dimensional or head-on collision.
Inelastic One Dimensional Collision
Applying Newton’s experimental law, we have
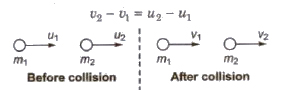
Velocities after collision
v1 = (m1 – m2) u1 + 2m2u2 / (m1 + m2)
and v2 = (m2 – m1) u2 + 2m1u1 / (m1 + m2)
When masses of two colliding bodies are equal, then after the collision, the bodies exchange their velocities.
v1 = u2 and v2 = u1
If second body of same mass (m1 = m2) is at rest, then after collision first body comes to rest and second body starts moving with the
initial velocity of first body.
v1 = 0 and v2 = u1
If a light body of mass m1 collides with a very heavy body of mass m2 at rest, then after collision.
v1 = – u1 and v2 = 0
It means light body will rebound with its own velocity and heavy body will continue to be at rest.
If a very heavy body of mass m1 collides with a light body of mass m2(m1 > > m21) at rest, then after collision
v1 = u1 and v2 = 2u1
In Inelastic One Dimensional Collision
Loss of kinetic energy
ΔE = m1m2 / 2(m1 + m2) (u1 – u2)2 (1 – e2)
In Perfectly Inelastic One Dimensional Collision
Velocity of separation after collision = 0.
Loss of kinetic energy = m1m2 (u1 – u2)2 / 2(m1 + m2)
If a body is dropped from a height ho and it strikes the ground with velocity vo and after inelastic collision it rebounds with velocity v1 and rises to a height h1, then
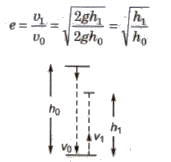
If after n collisions with the ground, the body rebounds with a velocity vn and rises to a height hn then
en = vn / vo = √hn / ho
Two Dimensional or Oblique Collision
If the initial and final velocities of colliding bodies do not lie along the same line, then the collision is called two dimensional or oblique Collision.
In horizontal direction,
m1u1 cos α1 + m2u2 cos α2= m1v1 cos β1 + m2v2 cos β2
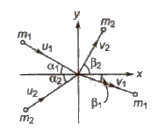
In vertical direction.
m1u1 sin α1 – m2u2 sin α2 = m1u1 sin β1 – m2u2 sin β2
If m1 = m2 and α1 + α2 = 90°
then β1 + β2 = 90°
If a particle A of mass m1 moving along z-axis with a speed u makes an elastic collision with another stationary body B of mass m2
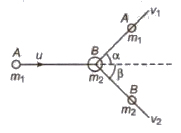
From conservation law of momentum
m1u = m1v1 cos α + m2v2 cos β
O = m1v1 sin α – m2v2 sin β
.png)