The branch of science which deals with the quantitative relationship between heat and other forms of energies is called thermodynamics.

Some Important Terms Related to Thermodynamics

(i) System It refers to the part of universe in which observations are carried out.

(ii) Surroundings The part of universe other than the system is known as surroundings.

(ill) Boundary The wall that separates the system from the surroundings is called boundary.

(iv) Thermodynamic equilibrium A system in which the macroscopic properties do not undergo any change with time is called thermodynamic equilibrium.

(v) Thermal equilibrium If there is no flow of heat from one portion of the system to another, the system is said to be in thermal equilibrium.

(vi) Mechanical equilibrium If no mechanical work is done by one part of the system on another part of the system. it is said to be in mechanical equilibrium. Such a condition exists when pressure remains constant.

Types of Systems

(i) Open system The system in which energy and matter both can be exchanged with the surroundings.

(ii) Closed system The system in which only energy can be exchanged with the surroundings.

(iii) Isolated system The system in which neither energy nor matter can be exchanged with the surroundings.

Thermodynamics Properties

1. Intensive Properties

Properties of the system which depend only on the nature of matter but not on the quantity of matter are called Intensive properties, e.g., pressure, temperature, specific heat, etc

2. Extensive Properties

Properties of the system which are dependent on the quantity of matter are called extensive properties, e.g., internal energy, volume, enthalpy, etc.

State of System

When microscopic properties have definite value, the conditions of existence of the system is known as state of system.

State functions When values of a system is independent of path followed and depend only on initial and final state, it is known as state function,e.g., Δ U, Δ H, Δ G etc.

Path functions These depend upon the path followed, e.g., work, heat, etc.

Thermodynamic Process

It is the operation which brings change in the state of the system.

Thermodynamic processes are

(i) Isothermal process In which temperature remains constant, i.e., (dT = 0, Δ U = 0).

(ii) Isochoric process In which volume remains constant, i.e., (Δ V = 0).

(iii) Isobaric process In which pressure remains constant, i.e., (Δp = 0).

(iv) Adiabatic process In which heat is not exchanged by system with the surroundings, i.e., (Δq = 0).

(v) Cyclic process It is a process in which system returns to its original state after undergoing a series of change, i.e., Δ U _cyclic = 0; Δ H _cyclic = 0

(vi) Reversible process A process that follows the reversible path, i.e., the process which occurs in infinite number of steps in this Way that the equilibrium conditions are maintained at each step, and the process can be reversed by infinitesimal change in the state of functions.

(vii) Irreversible process The process which cannot be reversed and amount of energy increases. All natural processes are Irreversible.

Internal Energy (E or U)

It is the total energy within the substance. It is the sum of many types of energies like vibrational energy, translational energy. etc. It is a extensive property and state function.

Its absolute value cannot be determined but experimentally change in internal energy (Δ) can be determined by

ΔU = U₂ – U₁ or ΣU_p – ΣU_R

For exothermic process, ΔU = -ve, whereas for endothermic process ΔU = +ve

U depends on temperature, pressure, volume and quantity of matter.

Zeroth Law of Thermodynamics or Law of Thermal Equilibrium

The law states that if the two systems are in thermal equilibrium with a third system then they are also in thermal equilibrium with each other. Temperature is used here to know, the system is in thermal equilibrium or not.

First Law of Thermodynamics

Energy can neither be created nor destroyed although it can be converted from one form to the other.

Mathematically, ΔU = q + W

where, ΔU = internal energy change

q = heat added to system

W = work added to system

Sign convention

(i) q is + ve = heat is supplied to the system

(ii) q is – ve = heat is lost by the system

(iii) Wis + ve = work done on the system

(iv) Wis – ve =work done by the system

Modes of Transference of Energy

Heat (q)

It occurs when there is a difference of temperature between system and surroundings. It is a random form of energy and path dependent. Its units are joule or calorie.

Work (W)

If the system involves gaseous substances and there is a difference of pressure between system and surroundings. work is referred as pressure – volume work (W_pV).

Expression for Pressure – Volume Work

(i) Work of Irreversible expansion against constant pressure B under isothermal conditions

W_pV = – p_ext ΔV

(ii) Work of reversible expansion under isothermal conditions

(iii) Work of reversible expansion under adiabatic conditions

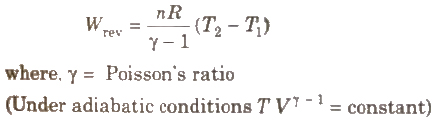
(iv) Work of irreversible expansion under adiabatic conditions

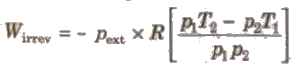
(v) When an ideal gas expands in vacuum then

p_ext = 0

Work done is maximum in reversible conditions

Units CGS system – erg

SI system – joule

Work and heat both appear only at the boundary of the system during a change in state.]

Heat Capacity of a System

Heat Capacity (c) of a system is defined as the amount of heat required to raise the temperature of a system by 1° C.

1. Molar Heat Capacity

It is the heat capacity 1 mole of substance of the system.

2. Specific Heat Capacity

It is the heat capacity of 1 g of substance of the system

q = mc Δ T.

where, m = mass of substance

c = specific heat or heat capacity

Molar heat capacity, at constant pressure,

C_p = C_p * M

Molar heat capacity. at constant volume

C_V = C_V * M

(c_p and C_V are specific heats at constant pressure and constant volume respectively and M is molecular weight of gas)

c_p – C_V = R (R = Molar gas constant)

C_p – C_V = R / M

The molar heat capacity at constant volume,

C_V = (3 / 2) R

The molar heat capacity at constant pressure,

C_p = (3 / 2) R + R = (5 / 2)R

Poisson’s ratio, γ = C_p / C_V = (5 / 3) = 1.66

γ = 1.66 for monoatomic gas

γ = 1.40 for diatomic gas

γ = 1.33 for triatomic gas

Enthalpy (H)

It is the sum of internal energy and pV-energy of the system. It is a state function and extensive property. Mathematically,

H = U + pV

Like U. absolute value of H also cannot be known, ΔH is determined experimentally.

ΔH = H₂ – H₁

or ΣH_p = ΣH_R

For exothermic reaction (the reaction in which heat is evolved), ΔH = -ve whereas for endothermic reaction (the reaction in which heat is absorbed), ΔH = +ve.

Relationship between ΔH and ΔU

ΔH = ΔU + Δp Δ V

or ΔH = ΔU + Δn_(g) RT

Here, Δn_(g) = change in the number of gas moles.

Enthalpy or Heat of Reaction (ΔrH)

It is the change in enthalpy that accompanies a chemical reaction represented by a balanced chemical equation.

ΔrH = ΣH_(p) – ΣH_(R)

Enthalpy of reaction expressed at the standard state conditions is called standard enthalpy of reaction (ΔH).

Factors affecting enthalpy of reaction

(i) Physical state of reactants and products.

(ii) Allotropic forms of elements involved.

(iii) Chemical composition of reactants and products.

(iv) Amount of reactants.

(v) Temperature.

Various Forms of Enthalpy of Reaction

1. Enthalpy of Formation (ΔH_f)

It is heat change when one mole of compound is obtained from Its constituent elements.

Enthalpy of formation at standard state is known as standard enthalpy of formation Δ_fH° and is taken as zero by convention. It also gives the idea of stability.

2. Enthalpy of Combustion

It is the Enthalpy change taking place when one mole of a compound undergoes complete combustion In the presence of oxygen (ΔH_c.)

ΔH_c because process of combustion is exothermic.

3. Enthalpy of Solution

It is the Enthalpy change when one mole of a substance is dissolved in large excess of solvent, so that on further dilution no appreciable heat change occur.

4. Enthalpy of Hydration

It is the enthalpy change when one mole of anhydrous substances undergoes complete combustion. It is an exothermic process.

5. Enthalpy of Fusion

It is the enthalpy change that accompanies melting of one mole of solid substance.

6. Enthalpy of Vaporisation

It is the enthalpy change that accompanies conversion of one mole of liquid substance completely into vapours.

7. Enthalpy of Neutralisation

It is the enthalpy change that takes place when 1 g-equivalent of an acid (or base) is neutralised by 1 g-equivalent of a base (or acid) in dilute solution.

Enthalpy of neutralisation of strong acid and strong base is always constant, i.e., 57.1 kJ.

[Enthalpy of neutralisation of strong acid and weak base or weak acid and strong base is not constant and numerically less than 57.1 kJ due to the fact that here the heat is used up in ionisation of weak acid or weak base. This is known as enthalpy of ionisation of weak acid / or base.]

8. Enthalpy of Transition

It is the enthalpy change when one mole of the substance undergoes transition from one allotropic form to another.

9. Enthalpy of Atomisation

It is the enthalpy change occurring when one mole of the molecule breaks into its atoms.

10. Enthalpy of Dilution

It is the enthalpy change, when one mole of a substance is diluted from one concentration to another.

11. Enthalpy of Sublimation

It is the enthalpy change, when one mole of a solid substance sublines.

12. Lattice Enthalpy

It is the enthalpy change, when one mole of an ionic compound dissociates into its ions in gaseous state.

Laws of Thermochemistry

1. Lavoisier Laplace Law

Th enthalpy change during a reaction is equal in magnitude to the enthalpy change in the reverse process but it is opposite in sign.

2. Hess’s Law of Constant Heat Summation

The standard enthalpy of a reaction. which takes place in several steps, is the sum of the standard enthalpIes of the intermediate reactions into which the overall reactions may be divided at the same temperature.

According to Hess’s law

ΔH = ΔH₁ + ΔH₂ + ΔH₃

Applications of Hess’s law are

(a) In determination of beat of formation.

(b) In determination of heat of transition.

(c) In determination of heat of hydration.

(d) To calculate bond energies.

3. Trouton’s Rule

According to this law, “The ratio of enthalpy of vaporization and normal boiling point of a liquid IS approximately equal to 88 J per mol per kelvin. i.e.,

ΔH_vap / T = 88 J / mol / K

4. Dulong and Petit Law

This law states “The product of specific heat and molar mass of any metallic element is equal to 6.4 cal/ mol/ °C. i.e.,

5. kirchhoff’s Equation

ΔC_p = ΔH₂ – ΔH₁ / T₂ – T₁

and ΔC_v = ΔE₂ – ΔE₁ / T₂ – T₁

6. Clausius – Clapeyron Equation

– 2.303 log p₂ / p₁ = ΔH_v / R (T₂ – T₁ / T₁ T₂)

where, ΔH_v = molar heat of vaporisation.

Bond Enthalpy

It is the average amount of energy required to break one mole of bonds in gaseous molecules.

Bond Dissociation Enthalpy

The energy required to break the particular bond in a gaseous molecule is called bond dissociation enthalpy. It is definite in quantity and expressed in kJ mol^-1.

In diatomic molecule, bond dissociation enthalpy = Bond enthalpy

In polyatomic molecule, bond dissociation enthalpy ≠ Bond Enthalpy

ΔH = [sum of bond enthalpies of reactants] – [sum of bond enthalpies of products]

Factors affecting bond enthalpy

(i) Size of atoms

(ii) Electronegativity

(iii) Bond length

(iv) Number of bonding electrons

Entropy (S)

It is the measurement of randomness or disorder of the molecules. It is a state function and extensive property.

Units : jK^-1 mol^-1

The change in entropy during a process is mathematically given as

Δ_rS° = Σ S° (products) – Σ S° (reactants) = q_rev / T = ΔH / T

Where, q_rev heat absorbed by the system in reversible manner

T = temperature

Δ S > 0, Increase in randomness, heat is absorbed

Δ S < 0, Decrease in randomness, heat is evolved.

Entropy of even elementary substances are not zero.

Entropy change of an ideal gas is given by

Δ S = _nC_V In (T₂ / T₁) + nR In (V₂ / V₁)

Entropy Change During Phase Transition

The change of matter from one state to another state is called phase transition.

The entropy changes at the time of phase transition:

Spontaneous Process

The physical or chemical process which proceeds by its own in a particular direction under given set of conditions without outside heir is called spontaneous process. It cannot be reversed.

All natural processes are spontaneous process.

Spontaneous process where no initiation is needed

(i) Sugar dissolves in water.

(ii) Evaporation of water.

(iii) Nitric oxide (NO) reacts with oxygen.

Spontaneous process where some initiation is required

(i) Coal keeps on burning once initiated.

(ii) Heating of CaCO₃ to give calcium oxide and CO₂ is initiated by heat.

Enthalpy Criterion of Spontaneous Process

All the processes which are accompanied by decrease of energy (exothermic reactions, having negative value of ΔH) occur spontaneously.

It fails when some endothermic reactions occur spontaneously.

Entropy Criterion of Spontaneous Process

A process is a spontaneous if and only if the entropy of the universe increases.

For a process to be Spontaneous

(ΔS_universe > 0 or ΔS_syst + ΔS_surr > 0)

At equilibrium state, ΔS = 0,

Limitations of ΔS criterion and need for another term We cannot find entropy change of surroundings during chemical changes. So we need another parameter for spontaneity viz Gibbs’ energy of system (G).

Second Law of Thermodynamics

The entropy of the universe is always Increasing in the course of every spontaneous or natural change.

Or

All spontaneous processes or natural change are thermodynamically irreversible without the help of an extemal work. i.e., heat cannot flow itself from a colder to hotter body.

Joule-Thomson Effect

The phenomenon of cooling of a gas when it is made to expand adiabatically from a region of high pressure to a region of extremely. low pressure is known as Joule-Thomson effect. This effect is zero when an ideal gas expands in vacuum.

[When an ideal gas undergoes expansion under adiabatic condition in vacuum, no change takes place in its internal energy, i.e., (∂E / ∂V)_T = 0 where, (∂E / ∂V)_T is called the Internal pressure.]

Joule-Thomson Coefficient

The number of degrees of temperature change produced per atmospheric drop in pressure at constant enthalpy when a gas is allowed to expand through a porous plug is called Joule-Thomson coefficient. It is given as

μ = dT / dp

where, μ = Joule-Thomson coefficient

dT = change in temperature

dp = change in pressure.

Inversion Temperature

The temperature below which a gas becomes cooler on expansion is known as the inversion temperature. It is given as

T_i = 2a / Rb

where, a and b = van der Waals’ constant

At inversion temperature T_i, the the Joule Thomson coefficient μ = 0, i.e., the gas neither heated nor cooled.

Carnot Cycle

It is an imaginary cycle which demonstrates the maximum conversion of heat into work. It involves four processes

(i) isothermal reversible expansion;

(ii) adiabatic reversible expansion;

(ii) adiabatic reversible expansion;

(iv) adiabatic reversible compression.

The efficiency of a heat engine in a Carnot cycle,

η = T₂ – T₁ / T₂

= q₂ – q₁ / q₂ = w / q₂

Gibbs Energy or Gibbs Free Energy

It is the energy available for a system at some conditions and by which useful work can be done. It is a state function and extensive property.

Mathematically,

G = H – TS

Change in Gibbs energy during the process 1S given by Gibbs Helmholtz equation.

(ΔG = G₂ – G₁ = ΔH – TΔS)

where, ΔG = Gibbs free energy

H = enthalpy of system

TS = random energy

ΔG_system = – TΔS_total

The Gibbs energy criterion of spontaneity

ΔG > 0, process is non-spontaneous

ΔG < 0, 0, process is spontaneous

ΔG = 0, process is in equilibrium state

Effect of Temperature on Spontaneity

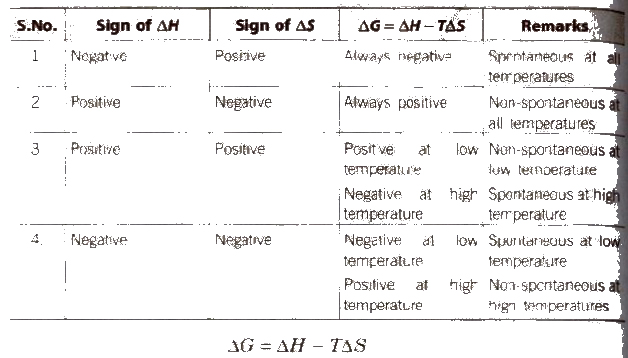
Now an exothermic reaction which is non-spontaneous at high temperature may become spontaneous at low temperature. Similarly, endothermic reactions which are non-spontaneous at low temperature may become spontaneous at high temperature.

Standard Free Energy Change (Δ G)

It is the change in free energy which takes places when the reactants are converted into products at the standard states, i.e., (1 atm and 298 K)

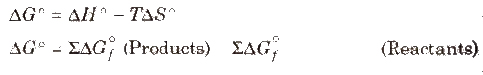
where, ΔG°_f = standard energy of formation

Standard energy of formation of all free elements is zero.

Gibbs Energy Change and Equilibrium

Criterion for equilibrium,

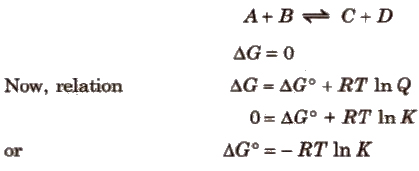
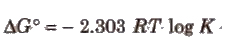
⇒ We also know that

Relation between ΔG° and EMF of the Cell

Third Law of Thermodynamics

This law was formulated by Nernst in 1906. According to this law, “The entropy of a perfectly crystalline substance at zero K or absolute zero is taken to be zero”. We can find absolute entropies of pure substances at different temperature.

where, C_p = heat capacities

T = temperature between 0 K and T K

This law is on1y applicable for perfectly crystalline substances. If there is imperfection at 0 K, the entropy will be larger than zero.