Hitherto five states of matter are known, viz, solid, liquid, gas, plasma and Bose-Einstein condensate. Out of these solid, liquid and gas are commonly found while remaining two are found only under specific
conditions.

Interconversion of States of Matter

These stateS are interconvertible.

(i) Melting point This is the temperature at which a matter converts from its solid state to liquid state. It decreases in the presence of impurity.

(ii) Boiling point This is the temperature at which the vapour” pressure of a liquid becomes equal to the atmospheric pressure. It increases in the presence of impurity and with rise in pressure. Boiling point of water is 100°C.

(iii) Freezing point At this temperature, a matter converts from its fluid state into solid state.

Freezing point of water is 0°C.

(iv) Evaporation It is the process of conversion of a liquid into vapours at any temperature.

Due to evaporation,

(a) water droplets appear on the outer surface of a glass containing ice-cold water.

(b) water kept in earthen pot becomes cool during summer.

(c) desert cooler cool better on a hot dry day.

In short,

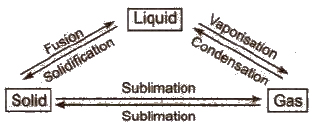
The temperature and pressure at which all the three states of a substance can exist together in equilibrium is called triple point, e.g.,
ice, liquid water and water vapours can coexist

(i. e., ice ⇔ water ⇔ vapour) at 0.0098°C and 4.58 mm.

Plasma

It is a state of matter similar to gas in which a certain portion of the gaseous particles are ionised. Because of the average strength of the electrical forces, the plasma is neutral. It is commonly found in the universe.

On earth, plasma is naturally occurring in flames, lightnings and the auroras.

Bose-Einstein Condensate

A Bose-Einstein condensate is a gaseous superfluid phase formed by atoms cooled to temperature very near to absolute zero.

This state was first predicted by Satyendra Nath Bose and Albert Einstein in 1924-25. Such first condensate was produced by Eric Cornell and Carl Wieman in 1995. It can be thought of as the opposite of a plasma.

Factors Deciding Physical State of a Substance

For gaseous state,

Forces of attraction << thermal energy For liquid state, Forces of attraction > Thermal energy

For solid state,

Forces of attraction >> Thermal energy

Intermolecular Forces

The forces of attraction existing among the molecules of a substance (gaseous, liquid or solid) are called intermolecular forces

[Greater the intermolecular forces, higher is the melting and boiling point.

Attractive intermolecular forces are known as van der Waals’ forces.]

The different types of intermolecular forces are briefly explained below

(i) Dipole-dipole interactions Dipole-dipole forces act between the molecules possessing permanent dipoles.

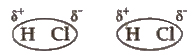
The interaction is stronger than London forces and weaker than ion-ion interaction.

(ii) Dipole-induced dipole forces Dipole-induced dipole forces act between the polar molecules having permanent dipole and the molecules lacking permanent dipole

(iii) Dispersion forces or London forces Dispersion forces or London forces are present among non-polar atoms and molecules, e.g., among the atoms or chlorine molecules. These are the weakest intermolecular forces. These forces increases with

(i) increase in number of electrons in molecules,

(ii) increase in molecular size

The Gaseous State

This is the simplest state of matter. Characteristics of this ‘state of matter are

1. In gases, the intermolecular forces are weakest.
2. Gases are highly compressible.
3. Gases exert pressure equally in all directions.
4. Gases have much lower density than the solids and liquids.
5. The volume and the shape of gases are not fixed.
6. Gases mix evenly and completely in all proportions without any mechanical aid.

Measurable Properties of Gases

(i) Mass It is expressed in gram or kg.

(ii) Volume It is equal to the volume of the container and is expressed in terms of litre (L), millilitre (mL), cubic centimetre (cm³), cubic metre (m³) or cubic decimetre (dm³).

1 L = 1000 mL = 1000 cm³ = 1 dm³

1 m³ = 10³ dm³ = 10⁶ cm³ = 10⁶ mL = 10³L

(iii) Pressure Gas pressure is measured with manometer and atmospheric pressure is measured by barometer.

1 atm = 76 em of Hg = 760 mm of Hg = 760 torr

1 atm = 101.325 kPa = 101325 Pa = 101.325 Nm^-2 = 1.01325 bar

1 bar = 10⁵ Pa.

Measurement of pressure of gas

(i) Open end manometer, p_gas = p_atom – h

(ii) Closed end manometer, p_gas = h

where h is difference in the mercury levels in the two columns of density (d) (of a gas).

(iv) Temperature It is measured in celsius scale (OC) or in Kelvin scale (K). SI unit of temperature is kelvin (K), T (K) = t°C+ 273

Standard temperature and pressure (STP or NTP) means 273.15 K (O°C) temperature and 1 bar (i.e., exactly 10⁵ pascal) pressure. At STP, molar volume of an ideal gas is 22.71098 L mol^-1

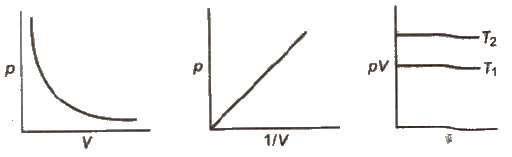
Boyle’s Law

The volume of a given mass of a gas is inversely proportional to its pressure at constant temperature.

V ∝ 1 / p or Vp = K

K is a constant and its value depends on mass, temperature and nature of gas.

∴ p₁V₁ = p₂V₂

Isotherms Graphs of V vs p or pV vs p at constant temperature known as Isotherms .

IAirisdense at the sea level because it is compressed by the mass of above it.

Charles’ Law

The volume of the given mass of a gas increases or decrease by 1 / 273 of its volume for each degree rise or fall of temperature respectively at constant pressure.

V_t = V_o (1 + t / 273) t constant p

or

The volume of a given mass of a gas is directly proportional to the absolute temperature at constant pressure.

V ∝ T (at constant p), V / T = constant or V₁ / T₁ = V₂ / T₂

Absolute zero is the theoretically possible temperature at which the volume of the gas becomes zero. It is equal to O°C or 273.15K.

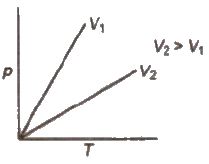
Isobars A graph of V vs T at constant pressure is known as isobar

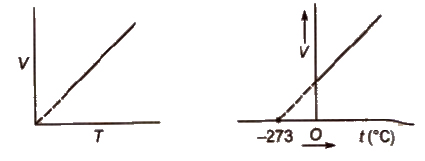
Charles’law explains that gases expand on heating, so hot air is less dense than cold air.

Gay Lussac’s Law

The pressure of a given mass of gas increases or decreases by 1 /273 of its pressure for each degree rise or fall of temperature respectively at constant volume.

p_t = p_o (1 + t / 273) at constant V and n

or

The pressure of a given mass of a gas at constant volume is directly proportional to absolute temperature.

p ∝ T or p = KT or p / T = K at constant V and n or P₁ / T₁ = P₂ / T₂

Isochores A graph of p vs T at constant volume is known as isochore

Avogadro’s Law

It states that equal volumes of all gases under the same conditions of temperature and pressure contain equal number of molecules.

Mathematically

V infi; n (at constant T and p)

or V / n = K

Molar gas volume The volume of one mole of a gas, i.e., 224 Lat STP(0°C, 1 atm) i_!S known as molar gas volume

Ideal Gas Equation

• V ∝1 / p, T and n constant (Boyle’s law)
• V ∝ T, p and n constant (Charles’ law)
• V ∝ n, p and T constant (Avogadro’s law)

⇒ V ∝ nT / p

or pV ∝ nT

or pV = nRT.

This is known as ideal gas equation. R is known as universal gas constant.

From the ideal gas equation, density.

d = pM / RT (where, M = molecular mass)

• ideal gas The gas which obeys the equation pV = nRT at every temperature and pressure range strictly Is known as Ideal gas.
• Real gases Since none of the gases present in universe strictly obey the equation pV =nRT. hence they are known as real or non-ideal gases. Real gases behave, ideally at low p and high T.

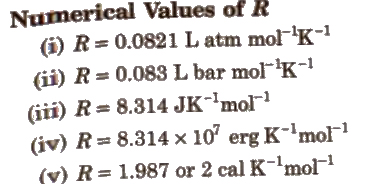
Graham’s Law of Diffusion

Under Similar conditions of temperature and pressure, the rates of diffusion of gases are inversely proportional to the square root of their densities.

Mathematically, r₁ / r₂ = √d₂ / √d₁ = √M₂ / √M₁

[Diffusion is the tendency of gases to distribute itself uniformly throughout the available space while effusion is the movement of gas through a small hole when it is subjected to pressure].

Dalton’s Law of Partial Pressure

At constant temperature. the total pressure. exerted by a mixture of non-reacting gases. is the sum of partial pressures of different gases present in the mixture.

p = p₁ + p₂ + p₃ + ….

partial pressure of a gas = mole fraction of the gas * total pressure.

If n₁, n₂ and n₃ are moles of non-reacting gases filled in a vessel of volume V at temperature T, the total pressure, p is given by

pV = (n₁ + n₂ + n₃)RT

This is the equation of state of a gaseous mixture,

[Aqueous tension It is the pressure exerted by water vapours at a particular temperature. It depends upon temperature.]

Pressure of a dry gas can be determined by Dalton’s law. When a gas is collected over water, its observed pressure is equal to the sum of the pressure of dry gas and the pressure of water vapour (aqueous tension) then

Pressure of dry gas = pressure of moist gas – aqueous tension.

Kinetic Theory of Gases

Main assumptions of this theory are:

1. A gas consists of large number of small particles, called molecules.

2. Volume occupied by gas molecules, is negligible as compared to the total volume of the gas.

3. There is continuous rapid random motion of gas molecules. The molecules collide with each other and with the walls of container.

4. The molecules are perfect elastic bodies and there is no loss of kinetic energy during collisions.

5. There are no attractive forces between the gaseous molecules.

6. The pressure exerted by a gas is due to the bombardment of gas molecules against the walls of the container.

7. The different molecules possess different velocities and hence, different energies. The average KE is directly proportional to absolute temperature.

KE = 3 / 2 RT

∴ Average kinetic energy per molecule = 3 / 2 kT

Here k is Boltzmann constant, it is gas constant per molecule.

k = R / N_A = 1.38 * 10^-23 JK^-1 mol^-1

From the above postulates, the kinetic gas equation derived is

pV = 1 / 3 mn U²

where, U = root mean square velocity = √3RT / M

Velocities of Gas Molecules

The different velocities possessed by gas molecules are :

(i) Most probable velocity (α) It is the velocity possessed by maximum fraction of gas molecules at a particular temperature.

α = √2RT / M

(ii) Average velocity (v) This is the average of the different velocities of all the molecules.

v = √8RT / πM

(iii) Root mean square velocity (U_rms) It is the square root of the mean of the square of the different velocities of the molecules.

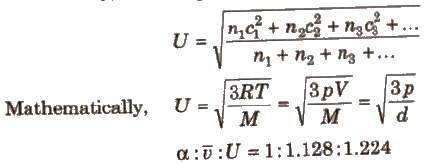
Deviation from Ideal Behaviour

At high pressure and low temperature, the gases deviate considerably from the ideal behaviour, Deviation can be expressed in terms of compressibility factor (Z), expressed as

Z = pV / nRT

In case of ideal gas, pV = nRT, Z = 1

In case of real gas, pV ≠ nRT, Z ≠ 1

Negative deviation In such case. Z < 1, gas is more compressible.

Positive deviation In such case. Z > 1 gas is less compressible.

The factors affecting the deviation are

(i) Nature of the gas In general. the most easily liquefiable and highly soluble gases show larger deviation.

(ii) Pressure The deviation is more at high pressure. CO₂ and N₂ show negative deviation at low pressure and positive derivation at high pressure.

(iii) Temperature The deviation is more at low temperature and H₂ and He always show positive deviations at O°C.

Cause of deviation from the ideal behaviour It is due to two faulty assumptions of kinetic theory of gases. particularly not valid at high pressure and low temperature

1. Volume occupied by the gas molecules is negligible as compared to the total volume of the gas.

2. There are no attractive forces between the gas molecules

van der Waals’ Equation

After volume and pressure correction, van der Waals’ obtained the following equation for n. moles of a gas.

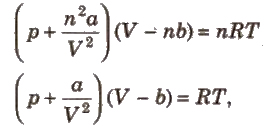
where,

b = excluded volume or co-volume = 4 * actual volume of gas molecules

a = magnitude of attractive forces between gas molecules.

The greater the value of ‘a’, the greater the strength of van der Waals’ forces and greater is the ease with which a gas can be liquefied.

Units for van der Waals’ constant

Pressure correction

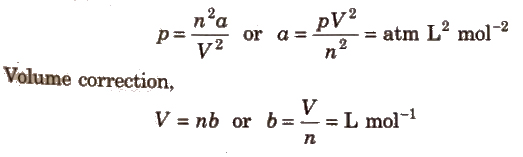
Limitation of van der Waals’ equation

There is specific range of temperature and pressure, to apply the equation. It deviates at very high pressure and very low temperature.

Liquefaction of Gases and Critical Points

The phenomenon of conversion of a gas into liquid is known as liquefaction. The liquefaction of a gas takes place when the intermolecular forces of attraction becomes so high that exist in the liquid. A gas can be liquefied by

(i) increasing pressure

(ii) decreaSing temperature

(i) Critical temperature (T_C) It may be defined as the temperature above which no gas can be liquefied. Critical temperature of CO₂ is 31.1° C.

Critical temperature (T_c) of some gases, He (5.4), H₂(33.2), N₂(126.0), CO(134.4), O₂ (154.3), CO₂(3041), NH₄(405.5).

T_C = 8a / 27Rb

(ii) Critical pressure (P_c) At critical temperature, the pressure needed to liquefy a gas is known as critical pressure.

P_c = a / 27 b²

(iii) Critical volume (V_c) The volume occupied by one mole of a gas at critical temperature and critical pressure is known as critical volume.

V_c = 3b

(iv) Boyle’s temperature (T_b) Temperature at which a real gas exhibits ideal behaviour for considerable range of pressure is called Boyle’s temperature.

T_b = a / bR

Liquid State

If a substance is having melting point below room temperature and boiling point above room temperature. the substance is known as liquid. In liquid state, matter has definite. shape and molecular motion is in between solids and gases.

Properties of Liquids

(i) Vapour pressure The pressure exerted by the vapours above the liquid surface when these are in equilibrium with the liquid at a given temperature is known as vapour pressure of liquid.

The vapour pressure of a liquid depends on :

(i) Nature of liquid

(ii) Temperature: Vapour pressure increases with increasing temperature.

(ii) Boiling point The temperature at which vapour pressure of liquids becomes equal to the atmospheric pressure, is called boiling point.

At 1 atm pressure, boiling point is known as normal boiling point.

At 1 bar pressure, boiling point is known as standard boiling point. Boiling point varies linearly with external pressure.

(iii) Surface tension It is the force acting per unit length perpendicular to the imaginary line drawn on the surface of liquid. It is denoted γ (gamma);

SI unit : Nm^-1

Dimensions: kgs^-2

The magnitude of surface tension of a liquid depends on the attractive forces between the molecules. It is measured with the help of an apparatus, called stalagmometer.

Surface tension decreases as the temperature increases.

Rise or fall of liquid in a capillary tube is due to surface tension.

(iv) Viscosity Viscosity is a measure of resistance to flow which arises due to friction between layers of fluid.

When there is a regular gradation of velocity, in passing from one layer to the next, it is called laminar flow.

F = η Adv / dz

where, F = forces required to maintain the flow of layers.

A = area of contact

dv/ dz = velocity gradient; (the change in velocity with distance.)

‘η’ is proportionality constant and is called coefficient of viscosity. Viscosity coefficient is the force when velocity gradient is unity and the area of contact is unit area. CGS unit of coefficient of viscosity is poise S.I. unit of coefficient of viscosity is Nsm^-2.