Cathode Rays

Cathode rays are the stream of fast moving electrons. These rays are produced in a discharge tube at a pressure below 0.01 rom of mercury.

Properties of Cathode Rays

(i) Cathode rays are not electromagnetic rays.

(ii) Cathode rays are deflected by electric field and magnetic field.

(iii) Cathode rays produce heat in metals when they fallon them.

(iv) Cathode rays can pass through thin aluminium or gold foils without puncturing them.

(v) Cathode rays can produce physical and chemical change.

(vi) Cathode ray travel in straight line with high velocity momentum and energy and cast shadow of objects placed in their path.

(vii) On striking the target of high atomic weight and high melting point, they produce X-rays.

(viii) Cathode rays produce fluorescence and phosphorescence in certain substance and hence affect photographic plate.

(ix) When any charge particle move in a field where magnetic and electric fields are present, without any deviation, then

Magnetic force = Electrostatic force

Bev = Ee or v = E / B

(x) Specific charge of cathode rays means the ratio of charge and mass.

(xi) Specific charge of electron was determined by J J Thomson using perpendicular magnetic and electric field applied on a beam of electrons, at the same place.

(xii) Specific charge of electron e / m = E² / 2VB²

where, E = electric field, B = magnetic field and V = potential difference applied across ends of tube.

(xii) The value of specific charge of an electron is 1.7589 * 10¹¹ C / kg.

(xiv) Millikan measured the charge of an electron through his popular oil drop experiment.

(xv) The charge of the electron as determined by Millikan was found to be 1.602 * 10^-19 C.

Positive Rays

Positive rays were discovered by Goldstein. Positive rays are moving positive ions of gas filled in the discharge tube. The mass of these particles is nearly equal to the mass of the atoms of gas.

(i) These consist of fast moving positively charged particles.

(ii) These rays are deflected in magnetic and electric fields.

(iii) These rays travel in straight line.

(iv) Speed of positive rays is less than that of cathode rays.

(v) These rays can produce fluorescence and phosphorescence.

Electron Emission

It is the phenomenon of emission of electron from the surface of a metal. The electron emission can be obtained from the following process

(i) Thermionic

(ii) Photoelectric emission

(iii) Field emission

(iv) Secondary emission

Photon

Photons are the packets of energy emitted by a source of radiation. The energy of each photon is,

E = hv

Where h is Planck’s constant and v is frequency of radiation.

The rest mass of a photon is zero.

The momentum of a photon p = hv / c = h / λ

Dynamic or kinetic mass 0f photon m = hv / c² = h / cλ

where c is speed of light in vacuum and λ is wavelength of radiation. Photons are electrically neutral.

A body can radiate or absorb energy in whose number multiples of a quantum hv, 2hv, 3hv …. nhv, where n is positive integer.

Photoelectric Effect

The phenomena of emission of electrons from a metal surface, when radiations of suitable frequency is incident on it, is called photoelectric effect.

Terms Related to Photoelectric Effect

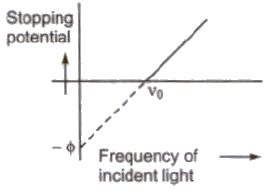
(i) Work Function(φ) The minimum amount of energy required to eject one electron from a metal surface, is called its work function.

(ii) Threshold Frequency (v_o) The minimum frequency of light which can eject photo electron from a metal surface is called threshold frequency of that metal.

(iii) Threshold Wavelength (λ_max) The maximum wavelength rJ light which can eject photo electron from a metal surface is called threshold wavelength of that metal.

Relation between work function, threshold frequency and threshold wavelength

φ = hv_o = hc / λ_max

Laws of Photoelectric Effect

1. For a given metal and frequency of incident light, the photo electric current (the rate of emission of photoelectrons) is directly proportional to the intensity of incident light.

2. For a given metal. there is a certain minimum frequency, called threshold frequency, below which there is no emission of photo electrons takes place.

3. Above threshold frequency the maximum kinetic energy of photo electrons depends upon the frequency of incident light.

4. The photoelectric emission is an instantaneous process.

Einstein’s Photoelectric Equation

The maximum kinetic energy of photoelectrons

(E_k)_max = hv – φ = h(v – v_o)

where v is frequency of incident light and v_o is threshold frequency.

Stopping Potential

The minimum negative potential given to anode plate at which photoelectric current becomes zero is called stopping potential (V_o).

Maximum kinetic energy of photo electrons

(E_k)_max = 1 / 2 mv²_max = eV_o

Compton Effect

When a monochromatic beam of X – falls on a target containing free electrons. it is scattered. As a result, the electrons recoil and scattered radiation has wavelength longer than incident one. This effect is called Compton effect.

(i) λ’ – λ = λ = Compton shift Δλ = h / m_oc (1 – cos φ) where m_o is rest mass of an electron and c is the speed of light h / m_oc Compton shift Δλ is maximum, when φ = 180°

(ii) Kinetic energy of recoil electron

E_k = hc / λ – hc / λ’

(iii) Direction of recoil electron

tan θ = λ sin φ / λ’ – λ cos φ

(iv) Compton wavelength of electron

= h / m_oc = 0.024 A

(v) Maximum Compton shift

(Δλ)_max = 2h / m_oc 0.0048 A

Matter Waves on de-Broglie Waves

A wave is associated with every moving particle, called matter or de-Broglie wave.

de-Broglie Wavelength

If a particle of mass m is moving with velocity v, then wavelength of de-Broglie wave associated with it is given by

λ = h / p = h / mv

de-Broglie wavelength of an electron is given by

λ = h / mv = h / √2me V = 12.27 / √V A.

where, m = mass of electron, e = electronic charge and V = potential difference with which electron is accelerated.

Davisson and Germer proves the existence of de-Broglie waves associated with an electron in motion.

Davisson-Germer Experiment

The wave nature of the material particles as predicted by de-Broglie was confirmed by Davisson and Germer (1927) in united states and by GP Thomson (1928) in scotland.

This experiment verified the wave nature of electron using Ni crystal.

Davisson and Germer found that the intensity of scattered beam of electrons was not the same but different at different angles of scattering. It is maximum for diffracting angle 50° at 54 V potential difference.

X-rays

When cathode rays strike on a heavy metal of high melting point. then a very small fraction of its energy converts in to a new type of waves, called X-rays.

Properties of X-rays

X-rays were discovered by Roentgen.

(i) X-rays are electromagnetic waves of wavelengths ranging from 0.1 A to 100 A and frequencies ranging from 10¹⁶ Hz to 10¹⁸ Hz.

(ii) Soft X-rays have greater wavelength and lower frequency.

(iii) Hard X-rays have lower wavelength and higher frequency.

(iv) X-rays are produced by coolidge tube.

(v) Molybdenum and tungsten provide suitable targets. These elements have large atomic number and high melting point for the purpose.

(vi) The intensity of X – rays depends on the heating voltage or filament current.

(vii) The kinetic energy of X-ray photons depends upon the voltage applied across the ends of coolidge tube.

(viii) Energy of X-ray photon is given by E = hv = hc / λ

(ix) If total energy of fast moving electron transfer to X-ray photon, then its energy, eV = hv = hc / λ

(x) Wavelength of emitted X-rays is given by λ = hc / eV

where, h = Planck’s constant, c = speed of light, e = electronic charge and V = potential difference applied across the ends of the tube.

(xi) Absorption of X-rays

I = I_oe^{– μx}, where I_o = initial intensity of X-rays, I = final intensity of emergent X-rays, x = thickness of material and μ = absorption coefficient.

Diffraction of X-rays

X-rays can be diffracted by crystals following Bragg’s law. According to which

2d sin θ = n λ

where, n = 1, 2, 3, …, and d = spacing of crystal planes, θ = angle of diffraction.

X-rays Spectrum

The energy spectrum of X-. rays is a line spectrum, containing following series :

(i) K – series When electrons of any higher orbit (n = 2,3,4, … ) jump to first orbit (n = 1) then K-series of X-rays are produced.

(ii) L – series When electrons of higher orbit (n = 3, 4, 5, … ) jump to second orbit (n = 2), then L-series of X-rays are produced.

(iii) M – series When electrons of higher orbit (n = 4,5,6, … )jump to third orbit (n = 3), then M-series of X-rays are produced.

First lines of these series are called K_α, L_α, M_α. Second lines of these series are called K_β, L_β, M_β

Moseley’s Law

The frequency of X-ray is given by

V = a (Z – b)²

where a and b are constants and Z is atomic number of element.

Frequency of X-rays

v ∝ Z²