





Projectile Motion
When any object is thrown from horizontal at an angle θ except 90°, then the path followed by it is called trajectory, the object is called projectile and its motion is called projectile motion.
If any object is thrown with velocity u, making an angle θ, from horizontal, then
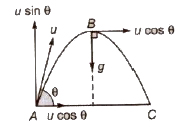
Important Points & Formulae of Projectile Motion
Time of flight It is defined as the total time for which the projectile remains in air.
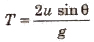
Maximum height It is defined as the maximum vertical distance covered by projectile.
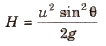
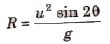
Horizontal range It is defined as the maximum distance covered in horizontal distance.
Note
(i) Horizontal range is maximum when it is thrown at an angle of 45° from the horizontal
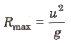
(ii) For angle of projections and (90° – 0) the horizontal range is same.
Projectile Projected from Some Heights
1. When Projectile is Projected Horizontally
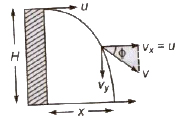
Initial velocity in vertical direction = 0
Time of flight T = √(2H/g)
Horizontal range x = uT = u √(2H/g)
Vertical velocity after t seconds
vy = gt (uy = 0)
Velocity of projectile after t seconds
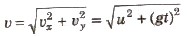
If velocity makes an angle φ, from horizontal, then
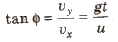
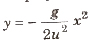
Equation of the path of the projectile
2. When Projectile Projected Downward at an Angle with Horizontal
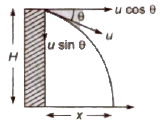
Initial velocity in horizontal direction = u cos θ
Initial velocity in vertical direction = u sin θ
Time of flight can be obtained from the equation,
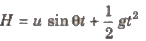
Horizontal range x = (u cos θ) t
Vertical velocity after t seconds
vy = u sin θ + gt
Velocity of projectile after t seconds
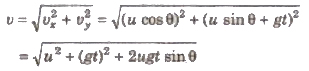
3. When Projectile Projected Upward at an Angle with Horizontal
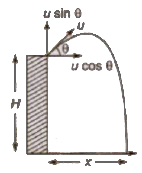
Initial velocity in horizontal direction = u cos θ
Initial velocity in vertical direction = u sin θ
Time of flight can be obtained from the equation
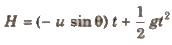
Horizontal range x = (u cos θ)t
Vertical velocity after t seconds, vy = (- u sin θ) + gt
Velocity of projectile after t seconcil
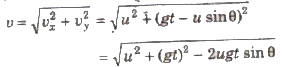
4. Projectile Motion on an Inclined Plane
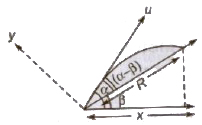
When any object is thrown with velocity u making an angle α from horizontal, at a plane inclined at an angle β from horizontal, then
Initial velocity along the inclined plane = u cos (α – β)
Initial velocity perpendicular to the inclined plane
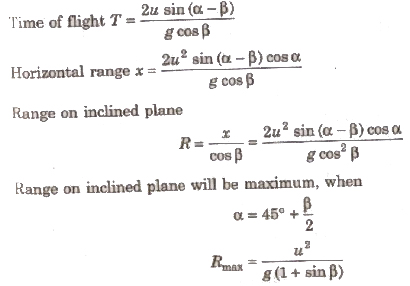
For angle of projections a and (90° – α + β), the range on inclined plane are same.
Circular Motion
Circular motion is the movement of an object in a circular path.
1. Uniform Circular Motion
If the magnitude of the velocity of the particle in circular motion remains constant, then it is called uniform circular motion.
2. Non-uniform Circular Motion
If the magnitude of the velocity of the body in circular motion is n constant, then it is called non-uniform circular motion.
Note A special kind of circular motion is when an object rotates around itself. This can be called spinning motion.
Variables in Circular Motion
(i) Angular Displacement Angular displacement is the angle subtended by the position vector at the centre of the circular path.
Angular displacement (Δθ) = (ΔS/r)
where Δs is the linear displacement and r is the radius. Its unit is radian.
(ii) Angular Velocity The time rate of change of angular displacement (Δθ) is called angular velocity.
Angular velocity (ω) = (Δθ/Δt)
Angular velocity is a vector quantity and its unit is rad/s.
Relation between linear velocity (v) and angular velocity (ω) is given by
v = rω
(iii) Angular Acceleration The time rate of change of angular velocity (dω) is called angular acceleration.

Its unit is rad/s2 and dimensional formula is [T-2].
Relation between linear acceleration (a) and angular acceleration (α).
a = rα
where, r = radius
Centripetal Acceleration
In circular motion, an acceleration acts on the body, whose direction is always towards the centre of the path. This acceleration is called centripetal acceleration.

Centripetal acceleration is also called radial acceleration as it acts along radius of circle.
Its unit is in m/s2 and it is a vector quantity.
Centripetal Force
It is that force which complex a body to move in a circular path.
It is directed along radius of the circle towards its centre.
For circular motion a centripetal force is required, which is not a new force but any force present there can act as centripetal force.
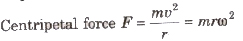
where, m = mass of the body, c = linear velocity,
ω = angular velocity and r = radius.
Work done by the centripetal force is zero because the centripetal force and displacement are at right angles to each other.
Examples of some incidents and the cause of centripetal force involved.
| S.No. | Incidents | Force providing Centripetal Force |
| 1 | Orbital motion of planets. | Gravitational force between planet and sun. |
| 2 | Orbital motion of electron. | Electrostatic force between electron and necleus. |
| 3 | Turning of vehicles at turn. | Frictional force acting between tyres of vehicle and road. |
| 4 | Motion of a stone in a circular path, tied with a string. | Tension in the string. |
Kinematical Equations in Circular Motion
Relations between different variables for an object executing circular motion are called kinematical equations in circular motion.
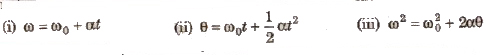
where, ω0 = initial angular velocity, ω = final angular velocity,
α = angular acceleration, θ = angular displacement and t = time.
Centrifugal Force
Centrifugal force is equal and opposite to centripetal force.
Under centrifugal force, body moves only along a straight line.
It appears when centripetal force ceases to exist.
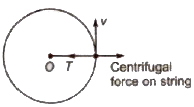
Centrifugal force does not act on the body in an inertial frame but arises as pseudo forces in non-inertial frames and need to be considered.
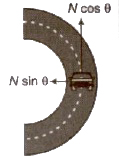
Turning at Roads
If centripetal force is obtained only by the force of friction between the tyres of the vehicle and road, then for a safe turn, the coefficient of friction (µs) between the road and tyres should be,
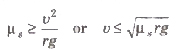
where, v = the velocity of the vehicle and r = radius of the circular path.
If centripetal force is obtained only by the banking of roads, then the speed (a) of the vehicle for a safe turn
v = √rg tan θ
If speed of the vehicle is less than √rg tan θ than it will move inward (down) and r will decrease and if speed is more than √rg tan θ, then it will move outward (up) and r will increase.
In normal life, the centripetal force is obtained by the friction force between the road and tyres as well as by the banking of the roads.
Therefore, the maximum permissible speed for the vehicle is much greater than the optimum value of the speed on a banked road. When centripetal force is obtained from friction force as well as banking of roads, then maximum safe value of speed of vehicle
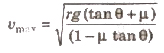
When a cyclist takes turn at road, he inclined himself from the vertical, slower down his speed and move on a circular path of larger radius.
If a cyclist inclined at an angle θ, then tan θ = (v2/rg)
where, v = speed of the cyclist, r = radius of path and g = acceleration due to gravity.
Motion in a Vertical Circle
(i) Minimum value of velocity at the highest point is √gr
(ii) The minimum velocity at the bottom required to complete the circle
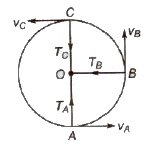
vA = √5gr
(iii) Velocity of the body when string is in horizontal position
vB = √3gr
(iv) Tension in the string
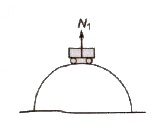
(v) When a vehicle is moving over a convex bridge, then at the maximum height, reaction (N1) is N1 = mg – (mv2/r)
(vi) When a vehicle is moving over a concave bridge, then at the lowest point, reaction (N2) is
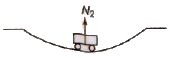
N2 = mg + (mv2/r)
(vii) When a car takes a turn, sometimes it overturns. During the overturning, it is the inner wheel which leaves the ground first.
(viii) A driver sees a child in front of him during driving a car, then it, better to apply brake suddenly rather than taking a sharp turn to avoid an accident.
Non-uniform Horizontal Circular Motion
In non-uniform horizontal circular motion, the magnitude of the velocity of the body changes with time.
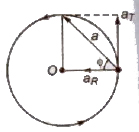
In this condition, centripetal (radial) acceleration (aR) acts towards centre and a tangential acceleration (aT) acts towards tangent. Both acceleration acts perpendicular to each other.
Resultant acceleration
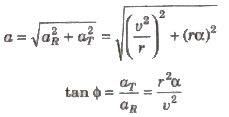
where, α is angular acceleration, r = radius and a = velocity.
Conical Pendulum
It consists of a string OA whose upper end 0 is fixed and bob is tied at the other free end. The string traces the surface of the cone, the arrangement is called a conical pendulum.
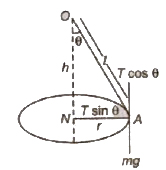
Time period of conical pendulum,
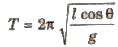
.png)