





Units.
Fundamental Units
Those physical quantities which are independent to each other are called fundamental quantities and their units are called fundamental units.
| S.No. | Fundamental Quantities | Fundamental Units | Symbol |
| 1. | Length | metre | m |
| 2. | Mass | kilogram | kg |
| 3. | Time | second | S |
| 4. | Temperature | kelvin | kg |
| 5 | Electric current | ampere | A |
| 6 | Luminous intensity | candela | cd |
| 7 | Amount of substance | mole | mol |
Supplementary Fundamental Units
Radian and steradian are two supplementary fundamental units. It measures plane angle and solid angle respectively.
| S.No. | Supplementary Fundamental Quantities | Supplementary Unit | Symbol |
| 1 | Plane angle | radian | rad |
| 2 | Solid angle | steradian | Sr |
Derived Units
Those physical quantities which are derived from fundamental quantities are called derived quantities and their units are called derived units.
e.g., velocity, acceleration, force, work etc.
Definitions of Fundamental Units
The seven fundamental units of SI have been defined as under.
Systems of Units
A system of units is the complete set of units, both fundamental and derived, for all kinds of physical quantities. The common system of units which is used in mechanics are given below:
Relationship between Some Mechanical SI Unit and Commonly Used Units
| S.No. | Physical Quantity | Unit | |
| 1 | Length | (a) | 1 micrometre = 10-6 m |
| (b) | 1 angstrom =10-10 m | ||
| 2 | Mass | (a) | 1 metric ton = 103 kg |
| (b) | 1 pound = 0.4537 kg | ||
| (c) | 1 amu = 1.66 x10-23 kg | ||
| 3 | Volume | 1 litre = 10-32 m3 | |
| 4. | Force | (a) | 1 dyne = 10-5 N |
| (b) | 1 kgf = 9.81 N | ||
| 5. | Pressure | (a) | 1 kgfm2 = 9.81Nm-2 |
| (b) | 1 mm of Hg = 133 Nm-2 | ||
| (c) | 1 pascal = 1 Nm-2 | ||
| (d) | 1 atmosphere pressure = 76 cm of Hg = 1.01 x 105 pascal | ||
| 6. | Work and energy | (a) | 1 erg =10-7 J |
| (b) | 1 kgf-m = 9.81 J | ||
| (c) | 1 kWh = 3.6 x 106 J | ||
| (d) | 1 eV = 1.6 x 10-19 J | ||
| 7. | Power | (d) | 1 kgf- ms-1 = 9.81W |
| 1 horse power = 746 W |
Some Practical Units
Some Approximate Masses
| Object | Kilogram |
| Our galaxy | 2 x 1041 |
| Sun | 2 x 1030 |
| Moon | 7 x 1022 |
| Asteroid Eros | 5 x 1015 |
Dimensions
Dimensions of any physical quantity are those powers which are raised on fundamental units to express its unit. The expression which shows how and which of the base quantities represent the dimensions of a physical quantity, is called the dimensional formula.
Dimensional Formula of Some Physical Quantities
| S.No. | Physical Quantity | Dimensional Formula | MKS Unit |
| 1 | Area | [L2] | metre2 |
| 2 | Volume | [L3] | metre3 |
| 3 | Velocity | [LT-1] | ms-1 |
| 4 | Acceleration | [LT-2] | ms-2 |
| 5 | Force | [MLT-2] | newton (N) |
| 6 | Work or energy | [ML2T-2] | joule (J) |
| 7 | Power | [ML2T-3] | J s-1 or watt |
| 8 | Pressure or stress | [ML-1T-2] | Nm-2 |
| 9 | Linear momentum or Impulse | [MLT-1] | kg ms-1 |
| 10 | Density | [ML-3] | kg m-3 |
| 11 | Strain | Dimensionless | Unitless |
| 12 | Modulus of elasticity | [ML-1T-2] | Nm-2 |
| 13 | Surface tension | [MT-2] | Nm-1 |
| 14 | Velocity gradient | T-1 | second-1 |
| 15 | Coefficient of velocity | [ML-1T-1] | kg m-1s-1 |
| 16 | Gravitational constant | [M-1L3T-2] | Nm2/kg2 |
| 17 | Moment of inertia | [ML2] | kg m2 |
| 18 | Angular velocity | [T-1] | rad/s |
| 19 | Angular acceleration | [T-2] | rad/S2 |
| 20 | Angular momentum | [ML2T-1] | kg m2S-1 |
| 21 | Specific heat | L2T-2θ-1 | kcal kg-1K-1 |
| 22 | Latent heat | [L2T-2] | kcal/kg |
| 23 | Planck’s constant | ML2T-1 | J-s |
| 24 | Universal gas constant | [ML2T-2θ-1] | J/mol-K |
Homogeneity Principle
If the dimensions of left hand side of an equation are equal to the dimensions of right hand side of the equation, then the equation is dimensionally correct. This is known as homogeneity principle.
Mathematically [LHS] = [RHS]
Applications of Dimensions
Significant Figures
In the measured value of a physical quantity, the number of digits about the correctness of which we are sure plus the next doubtful digit, are called the significant figures.
Rules for Finding Significant Figures
Significant Figures in Algebric Operations
(i) In Addition or Subtraction In addition or subtraction of the numerical values the final result should retain the least decimal place as in the various numerical values. e.g.,
If l1= 4.326 m and l2 = 1.50 m
Then, l1 + l2 = (4.326 + 1.50) m = 5.826 m
As l2 has measured upto two decimal places, therefore
l1 + l2 = 5.83 m
(ii) In Multiplication or Division In multiplication or division of the numerical values, the final result should retain the least significant figures as the various numerical values. e.g., If length 1= 12.5 m and breadth b = 4.125 m.
Then, area A = l x b = 12.5 x 4.125 = 51.5625 m2
As l has only 3 significant figures, therefore
A= 51.6 m2
Rules of Rounding Off Significant Figures
Error
The lack in accuracy in the measurement due to the limit of accuracy of the instrument or due to any other cause is called an error.
1. Absolute Error
The difference between the true value and the measured value of a quantity is called absolute error.
If a1 , a2, a3 ,…, an are the measured values of any quantity a in an experiment performed n times, then the arithmetic mean of these values is called the true value (am) of the quantity.
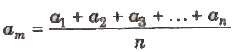
The absolute error in measured values is given by
Δa1 = am – a1
Δa2 = am – a1
………….
Δam = Δam – Δan
2. Mean Absolute Error
The arithmetic mean of the magnitude of absolute errors in all the measurement is called mean absolute error.
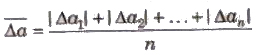
3. Relative Error The ratio of mean absolute error to the true value is called relative
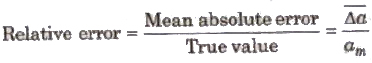
4. Percentage Error The relative error expressed in percentage is called percentage error.
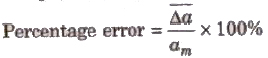
Propagation of Error
(i) Error in Addition or Subtraction Let x = a + b or x = a – b
If the measured values of two quantities a and b are (a ± Δa and (b ± Δb), then maximum absolute error in their addition or subtraction.
Δx = ±(Δa + Δb)
(ii) Error in Multiplication or Division Let x = a x b or x = (a/b).
If the measured values of a and b are (a ± Δa) and (b ± Δb), then maximum relative error
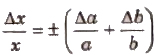
.png)